题目内容
【题目】已知函数![]() 的两个极值点为
的两个极值点为![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 在
在![]() (其中
(其中![]() 上是单调函数, 求
上是单调函数, 求![]() 的取值范围;
的取值范围;
(3)当![]() 时, 求证:
时, 求证:![]() .
.
【答案】(1)![]() (2)
(2)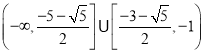 (3)详见解析
(3)详见解析
【解析】
试题分析:(1)由极值定义得![]() 得两根为
得两根为![]() ,由韦达定理得
,由韦达定理得![]() ,解得
,解得![]() ,再根据二次方程求根公式得
,再根据二次方程求根公式得![]() (2)由(1)可得函数有三个单调区间,由于
(2)由(1)可得函数有三个单调区间,由于![]() ,所以
,所以![]() 为单调区间的一个子集,即
为单调区间的一个子集,即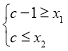 或
或![]() ,(3)利用不等式乘积性质证明不等式:利用导数可得
,(3)利用不等式乘积性质证明不等式:利用导数可得![]() 先将后增,有最小值
先将后增,有最小值![]() 所以
所以![]() ;根据二次函数最值得
;根据二次函数最值得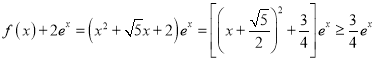 ,由于两个不等式中等号取法不一致,所以乘积中等号取不到
,由于两个不等式中等号取法不一致,所以乘积中等号取不到
试题解析:(1)![]() 由
由![]()
得![]() ,
,
![]() 由
由![]() 得
得![]() .
.
(2)由(1)知,![]() 在
在![]() 上递减, 在
上递减, 在![]() 上递增, 其中
上递增, 其中![]() ,
,
当![]() 在
在![]() 上递减时,
上递减时,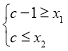 , 又
, 又![]() ,当
,当![]() 在
在![]() 上递增时,
上递增时,![]() , 综上,
, 综上, ![]() 的取值范围为
的取值范围为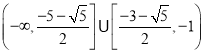 .
.
(3)证明: 设![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.![]() ,
,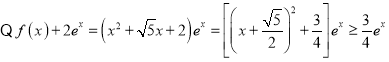 (当
(当![]() 时取等号),
时取等号),
![]() 不等式成立(因为取等条件不相同, 所以等号取不到).
不等式成立(因为取等条件不相同, 所以等号取不到).

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】中央电视台电视公开课《开讲了》需要现场观众,先邀请甲、乙、丙、丁四所大学的40名学生参加,各大学邀请的学生如下表所示:
大学 | 甲 | 乙 | 丙 | 丁 |
人数 | 8 | 12 | 8 | 12 |
从这40名学生中按分层抽样的方式抽取10名学生在第一排发言席就座.
(1)求各大学抽取的人数;
(2)从(1)中抽取的乙大学和丁大学的学生中随机选出2名学生发言,求这2名学生来自同一所大学的概率.



