题目内容
在数列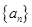 中,
中,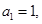 且对任意的
且对任意的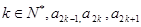 成等比数列,其公比为
成等比数列,其公比为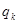 ,
,
(1)若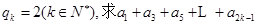 ;
;
(2)若对任意的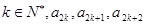 成等差数列,其公差为
成等差数列,其公差为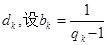 .
.
①求证: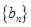 成等差数列,并指出其公差;
成等差数列,并指出其公差;
②若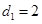 ,试求数列
,试求数列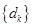 的前
的前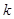 项和
项和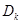 .
.
(1) ;(2)①
;(2)① ;②
;② 或
或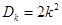
解析试题分析:(1)由于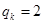
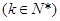 ,因此
,因此 成等比数列,且公比为4,故和易求;(2)①要证明
成等比数列,且公比为4,故和易求;(2)①要证明 是等差数列,就是要证明
是等差数列,就是要证明 为常数,也就是要找到
为常数,也就是要找到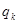 与
与 的关系,我们从唯一的已知条件有
的关系,我们从唯一的已知条件有 即
即 ,这就是
,这就是 变形为
变形为 即
即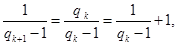 由此就证得
由此就证得
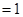 ;②求数列
;②求数列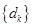 的前
的前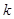 项和
项和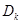 ,必须先求出通项
,必须先求出通项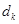 ,而
,而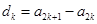 ,因此又应该求出
,因此又应该求出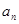 ,这时我们来看看已知
,这时我们来看看已知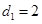 可得出什么?由
可得出什么?由 得
得 即
即 ,解得:
,解得: 或
或 ,从而可求得
,从而可求得 ,于是可通过
,于是可通过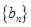 是公差为1的等差数列,求出
是公差为1的等差数列,求出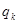 ,下面我们想办法通过
,下面我们想办法通过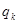 把
把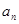 联系起来,
联系起来, ,于是
,于是
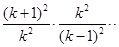
 ,而再用
,而再用 可得出
可得出 ,所以
,所以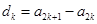 ,那么
,那么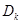 可求.
可求.
试题解析:(1)因为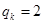 ,所以
,所以 (1分)
(1分)
故 是首项为1,公比为4的等比数列,
是首项为1,公比为4的等比数列,
所以 (4分)
(4分)
(2)①因为 成等差数列,所以
成等差数列,所以
而 所以
所以 (6分)
(6分)
则 得
得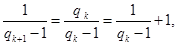
所以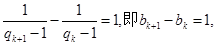 所以
所以 是等差数列,且公差
是等差数列,且公差 是等差数列,且公差为1.
是等差数列,且公差为1. 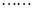 (9分)
(9分)
②因为 所以
所以 则由
则由 ,解得:
,解得: 或
或 。
。
(11分)
(i) 当 时,
时, ,所以
,所以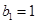 ,则
,则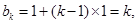 即
即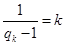 ,得
,得 ,所以
,所以
则
所以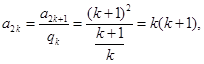 (13分)
(13分)
则 ,故
,故 ;(
;(

练习册系列答案
相关题目
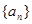 满足
满足 (
( ).
). ,
, (
( 和
和 的值,使得数列
的值,使得数列 为等比数列;并求此时数列
为等比数列;并求此时数列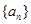 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 是
是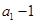 和
和 的等比中项,求:
的等比中项,求: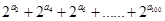 .
.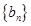 中的
中的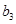 、
、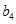 、
、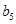 .
. ,求证:数列
,求证:数列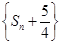 是等比数列.
是等比数列.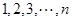 中这
中这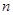 个数中取
个数中取 (
( ,
,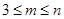 )个数组成递增等差数列,所有可能的递增等差数列的个数记为
)个数组成递增等差数列,所有可能的递增等差数列的个数记为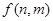 .
.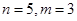 时,写出所有可能的递增等差数列及
时,写出所有可能的递增等差数列及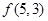 的值;
的值;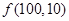 ;
;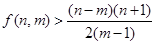 .
. 中,
中,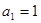 ,
,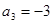 .
.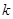 项和
项和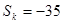 ,求
,求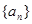 的公差不为零,其前n项和为
的公差不为零,其前n项和为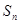 ,若
,若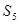 =70,且
=70,且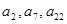 成等比数列,
成等比数列,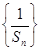 的前n项和为
的前n项和为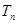 ,求证:
,求证: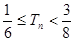 .
.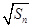 }都是等差数列,且公差相等.
}都是等差数列,且公差相等.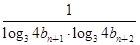 ,数列{cn}的前n项和为Tn,求Tn.
,数列{cn}的前n项和为Tn,求Tn.