题目内容
已知函数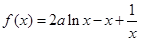 (
( 且
且 ),
),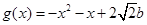
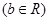 .
.
(1)若 在定义域上有极值,求实数
在定义域上有极值,求实数 的取值范围;
的取值范围;
(2)当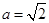 时,若对
时,若对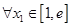 ,总
,总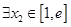 ,使得
,使得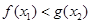 ,求实数
,求实数 的取值范围;(其中
的取值范围;(其中 为自然对数的底数)
为自然对数的底数)
(3)对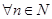 ,且
,且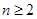 ,证明:
,证明: 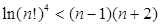 .
.
(1) ;(2)
;(2)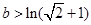 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)这是导数应用的常规题,值得注意的是 在定义域上有极值,等价于
在定义域上有极值,等价于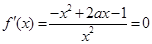 在定义域内有两个不等的根,而不是
在定义域内有两个不等的根,而不是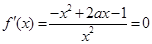 在定义域内有解;(2)分析题意,将问题成功地进行等价转化,转化为
在定义域内有解;(2)分析题意,将问题成功地进行等价转化,转化为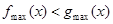 是解决问题的关键,接下来就是运用导数知识求两个函数的最值,并进行比较得出参数
是解决问题的关键,接下来就是运用导数知识求两个函数的最值,并进行比较得出参数 的取值范围;(3)这是赋有挑战性的一个,详见解析,但是我们要从中吸取一些对今后解题有帮助的东西,并注意一些知识的积累,如对
的取值范围;(3)这是赋有挑战性的一个,详见解析,但是我们要从中吸取一些对今后解题有帮助的东西,并注意一些知识的积累,如对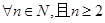 ,总有
,总有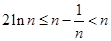 成立,它是如何证明的,从中知道是运用导数知识证明的,它又有什么作用,可以运用不等式的性质推导出一些新的不等式,这些对今后解题是很有帮助的.
成立,它是如何证明的,从中知道是运用导数知识证明的,它又有什么作用,可以运用不等式的性质推导出一些新的不等式,这些对今后解题是很有帮助的.
试题解析:(1) 的定义域为
的定义域为 ,要
,要 在定义域内有极值,则
在定义域内有极值,则 有两不等正根,即
有两不等正根,即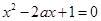 有两不等正根
有两不等正根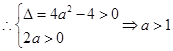 4分
4分
(2)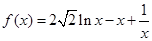 ,要对
,要对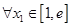 ,总
,总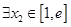 ,使得
,使得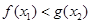
则只需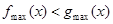 ,由
,由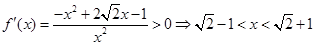 得函数
得函数 在
在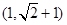 上递增,在
上递增,在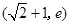 上递减,所以函数
上递减,所以函数 在
在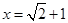 处有最大值; 6分
处有最大值; 6分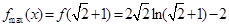 ,又
,又 在
在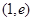 上递减,故
上递减,故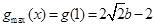
故有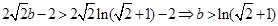 9分
9分
(3)当 时,
时,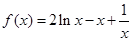 ,
,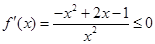 恒成立,故
恒成立,故 在定义域
在定义域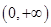 上单调递减,故当
上单调递减,故当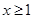 时,
时,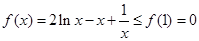 即
即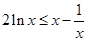 12分
12分
所以对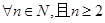 ,总有
,总有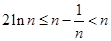 ,故有
,故有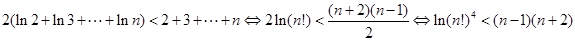 14分
14分
考点:1.导数的应用;2.参数范围;3.不等式证明.

练习册系列答案
相关题目
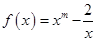 且
且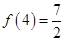 ,
, 的值;
的值; 在
在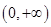 上的单调性,并用定义给予证明.
上的单调性,并用定义给予证明.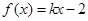 满足
满足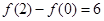 。
。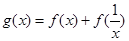 的值域。
的值域。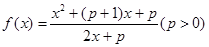 和
和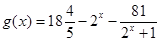 的定义域都是[2,4].
的定义域都是[2,4].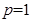 ,求
,求 的最小值;
的最小值;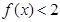 在其定义域上有解,求
在其定义域上有解,求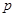 的取值范围;
的取值范围;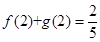 ,求证
,求证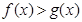 .
.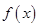 是定义在
是定义在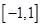 上的奇函数,在
上的奇函数,在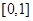 上
上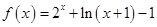 .
.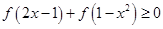 .
.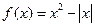 ,若
,若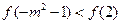 ,则实数
,则实数 的取值范围是 .;
的取值范围是 .;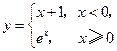 的反函数是__________.
的反函数是__________.