题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,求
,求![]() 的值;
的值;
(3)设![]() ,
,![]() 是函数
是函数![]() 图象上任意不同的两点,线段
图象上任意不同的两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .证明:
.证明:![]() .
.
【答案】(1)见解析;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】分析:(1)由条件可得![]() ,要求函数
,要求函数![]() 的单调区间,函数
的单调区间,函数![]() 的定义域为
的定义域为![]() 。求导得
。求导得![]() 。当
。当![]() 时,
时,![]() 。可得函数
。可得函数![]() 在
在![]() 上递增。(2)由函数
上递增。(2)由函数![]() 在区间
在区间![]() 上的最小值是
上的最小值是![]() ,可根据函数的单调性求函数的最小值,根据最小值等于
,可根据函数的单调性求函数的最小值,根据最小值等于![]() ,得到关于
,得到关于![]() 的关系式,即可求
的关系式,即可求![]() 。由(1)知
。由(1)知![]() 。因为
。因为![]() ,解不等式
,解不等式![]() ,
,![]() ,进而可得函数
,进而可得函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,进而可得
上递增,进而可得![]() ,所以
,所以![]() ,进而解得
,进而解得![]() 。满足
。满足![]() 。(3)要证明
。(3)要证明![]() ,应先把
,应先把![]() 和
和![]() 表示出来。由两点连线的斜率公式可得直线
表示出来。由两点连线的斜率公式可得直线![]() 的斜率为
的斜率为![]() ,由线段
,由线段![]() 的中点为
的中点为![]() ,可得
,可得![]() 。根据导函数可得
。根据导函数可得![]() 。所以要证
。所以要证![]() ,即证
,即证![]() 。以下利用分析法可证。不妨设
。以下利用分析法可证。不妨设![]() ,即证
,即证![]() ,即证
,即证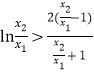 。把
。把![]() 看成整体。设
看成整体。设![]() ,即证
,即证![]() ,移项即证
,移项即证![]() ,其中
,其中![]() 。构造函数
。构造函数![]() 。证明函数的最小值大于0即可,求导数判断函数的单调性,进而求函数的最小值。
。证明函数的最小值大于0即可,求导数判断函数的单调性,进而求函数的最小值。
详解:(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
故函数![]() 在
在![]() 上递增。
上递增。
(2)由(1)知![]()
因为![]() ,
,
所以由![]() ,可得
,可得![]() ;
;
由![]() ,可得
,可得![]() 。
。
所以函数![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
所以![]() 。
。
所以![]() ,
,
解得![]() ,符合题意。
,符合题意。
(3)证明:由已知可得![]()
又![]() ,所以
,所以![]() 。
。
要证![]() ,即证
,即证![]() 。
。
不妨设![]() ,即证
,即证![]() ,即证
,即证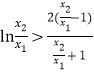 。
。
设![]() ,即证
,即证![]() ,
,
即证![]() ,其中
,其中![]() 。
。
设![]() ,
,
则![]()
所以![]() 在
在![]() 上单调递增,
上单调递增,
因此![]() 得证.
得证.

【题目】微信是现代生活进行信息交流的重要工具,据统计,某公司![]() 名员工中
名员工中![]() 的人使用微信,其中每天使用微信时间在一小时以内的有
的人使用微信,其中每天使用微信时间在一小时以内的有![]() ,其余的员工每天使用微信的时间在一小时以上,若将员工分成青年(年龄小于
,其余的员工每天使用微信的时间在一小时以上,若将员工分成青年(年龄小于![]() 岁)和中年(年龄不小于
岁)和中年(年龄不小于![]() 岁)两个阶段,那么使用微信的人中
岁)两个阶段,那么使用微信的人中![]() 是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,那么经常使用微信的员工中
是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,那么经常使用微信的员工中![]() 是青年人.
是青年人.
(1)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出![]() 列联表:
列联表:
青年人 | 中年人 | 总计 | |
经常使用微信 | |||
不经常使用微信 | |||
总计 |
(2)由列联表中所得数据判断,是否有百分之![]() 的把握认为“经常使用微信与年龄有关”?
的把握认为“经常使用微信与年龄有关”?
| 0.010 | 0.001 |
| 6.635 | 10.828 |
附:![]()
【题目】某校高二年级共有800名学生参加2019年全国高中数学联赛江苏赛区初赛,为了解学生成绩,现随机抽取40名学生的成绩(单位:分),并列成如下表所示的频数分布表:
分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
⑴试估计该年级成绩不低于90分的学生人数;
⑵成绩在![]() 的5名学生中有3名男生,2名女生,现从中选出2名学生参加访谈,求恰好选中一名男生一名女生的概率.
的5名学生中有3名男生,2名女生,现从中选出2名学生参加访谈,求恰好选中一名男生一名女生的概率.



