题目内容
【题目】如图,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上的一点,且
上的一点,且![]() ,
,![]() ,将矩形
,将矩形![]() 卷成以
卷成以![]() ,
,![]() 为母线的圆柱的半个侧面,且
为母线的圆柱的半个侧面,且![]() ,
,![]() 分别为圆柱的上、下底面的直径.
分别为圆柱的上、下底面的直径.
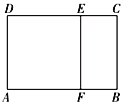
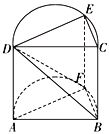
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据直径所对圆周角是直角,证得![]() ,根据圆柱侧棱和底面垂直,证得
,根据圆柱侧棱和底面垂直,证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,进而证得平面
,进而证得平面![]() 平面
平面![]() .
.
(2)首先证得![]() 平面
平面![]() ,即
,即![]() 是四棱锥
是四棱锥![]() 的高,再根据锥体体积公式,计算出四棱锥
的高,再根据锥体体积公式,计算出四棱锥![]() 的体积.
的体积.
(1)证明:∵![]() 在下底面圆周上,且
在下底面圆周上,且![]() 为下底面半圆的直径,∴
为下底面半圆的直径,∴![]() ,
,
由题设知,![]() ,又
,又![]() 为圆柱的母线,
为圆柱的母线,
∴![]() 垂直于圆柱的底面,
垂直于圆柱的底面,
则![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)解:设圆柱的底面半径为![]() ,
,
由题设知,![]() ,∴
,∴![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,![]() ,
,
由(1)知,![]() 平面
平面![]() ,
,
∴![]() 为四棱锥
为四棱锥![]() 的高,
的高,
又![]() ,
,
∴![]()
![]() .
.

练习册系列答案
相关题目
【题目】某市组织高三全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如下:
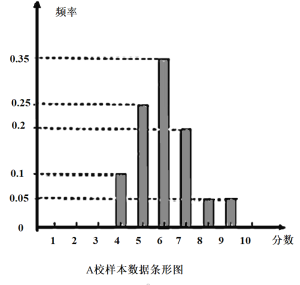
B校样本数据统计表:
成绩(分) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
人数(个) | 0 | 0 | 0 | 9 | 12 | 21 | 9 | 6 | 3 | 0 |
(1)计算两校样本数据的均值和方差,并根据所得数据进行比较.
(2)从A校样本数据成绩分别为7分、8分和9分的学生中按分层抽样方法抽取6人,若从抽取的6人中任选2人参加更高一级的比赛,求这2人成绩之和大于或等于15的概率.