题目内容
【题目】已知椭圆![]() :
:![]() (
(![]() )的右焦点为
)的右焦点为![]() ,离心率为
,离心率为![]() .直线
.直线![]() 过点
过点![]() 且不平行于坐标轴,
且不平行于坐标轴,![]() 与
与![]() 有两个交点
有两个交点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)证明:直线![]() 的斜率与
的斜率与![]() 的斜率的乘积为定值;
的斜率的乘积为定值;
(3)延长线段![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,若四边形
,若四边形![]() 为平行四边形,求此时直线
为平行四边形,求此时直线![]() 的斜率.
的斜率.
【答案】(1)![]() .(2)证明见解析.(3)直线
.(2)证明见解析.(3)直线![]() 的斜率:
的斜率:![]()
【解析】
(1)由题意知![]() ,
,![]() ,可得
,可得![]() ,
,![]() ,
,![]() .故得到椭圆方程.
.故得到椭圆方程.
(2)设直线![]() 的方程为
的方程为![]() (
(![]() ),将直线与椭圆进行联立,利用中点坐标公式,结合韦达定理得到
),将直线与椭圆进行联立,利用中点坐标公式,结合韦达定理得到![]() ,进而得解.
,进而得解.
(3)四边形![]() 为平行四边形,则
为平行四边形,则![]() .所以
.所以![]() ,
,
![]() ,又因为点
,又因为点![]() 在圆上,把点
在圆上,把点![]() 坐标代入椭圆方程,即可得出答案.
坐标代入椭圆方程,即可得出答案.
(1)由已知![]() ,
,![]() ,
,
又![]() ,解得
,解得![]() ,
,![]()
所以椭圆方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() (
(![]() )
)
联立 消去
消去![]() 得
得
![]() ,不妨设
,不妨设![]() ,
,![]()
则![]() ,因为
,因为![]() 为线段
为线段![]() 的中点
的中点
所以![]() ,
,![]()
所以![]()
所以![]() 为定值.
为定值.
(3)若四边形![]() 为平行四边形,则
为平行四边形,则![]()
所以![]()
![]()
因为点![]() 在椭圆上,所以
在椭圆上,所以
解得![]() ,即
,即![]()
所以当四边形![]() 为平行四边形时,直线
为平行四边形时,直线![]() 的斜率为
的斜率为![]()

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】第7届世界军人运动会于2019年10月18日至27日在湖北武汉举行,赛期10天,共设置射击、游泳、田径、篮球等27个大项,329个小项,共有来自100多个国家的近万名现役军人同台竞技.前期为迎接军运会顺利召开,特招聘了3万名志愿者.某部门为了了解志愿者的基本情况,调查了其中100名志愿者的年龄,得到了他们年龄的中位数为34岁,年龄在![]() 岁内的人数为15人,并根据调查结果画出如所示的频率分布直方图:
岁内的人数为15人,并根据调查结果画出如所示的频率分布直方图:
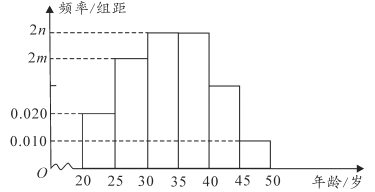
(1)求![]() ,
,![]() 的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
的值并估算出志愿者的平均年龄(同一组的数据用该组区间的中点值代表);
(2)本次军运会志愿者主要通过直接到武汉军运会执委会志愿者部现场报名和登录第七届世界军运会官网报名,即现场和网络两种方式报名调查.这100位志愿者的报名方式部分数据如下表所示,完善下面的表格,通过计算说明能否在犯错误的概率不超过0.001的前提下,认为“选择哪种报名方式与性别有关系”?
男性 | 女性 | 总计 | |
现场报名 | 50 | ||
网络报名 | 31 | ||
总计 | 50 |
参考公式及数据: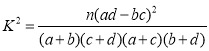 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
3.841 | 6.635 | 7.879 | 10.828 |