题目内容
【题目】某消费者协会在3月15号举行了以“携手共治，畅享消费”为主题的大型宣传咨询服务活动，着力提升消费者维权意识.组织方从参加活动的1000名群众中随机抽取n名群众，按他们的年龄分组：第1组
，第2组
，第3组
，第4组
，第5组
，其中第1组有6人，得到的频率分布直方图如图所示.
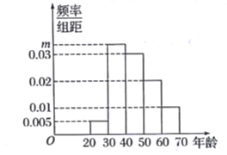
（1）求m，n的值，并估计抽取的n名群众中年龄在
的人数；
（2）已知第1组群众中男性有2人，组织方要从第1组中随机抽取3名群众组成维权志愿者服务队，求至少有两名女生的概率.
【答案】（1）
，
，年龄在
的人数为
（2）
【解析】
（1）根据第一组的频数和频率可得
，由所有频率和为1可得
，再求得
间的频率后可得人数；
（2）把第一组人数编号，如男性为
，女性为
，然后用列举法写出任取3人的所有基本事件及至少有两名女生的基本事件，计数后可得所求概率．
（1）
，
设第2组
的频率为f，
，
所以
，
第3组和第4组的频率为
，
年龄在的人数为
；
（2）记第1组中的男性为，女性为，
随机抽取3名群众的基本事件是：
，
，
共20种；
其中至少有两名女性的基本事件是：
共16种.
所以至少有两名女性的概率为
.
【题目】在十九大“建设美丽中国”的号召下，某省级生态农业示范县大力实施绿色生产方案，对某种农产品的生产方式分别进行了甲、乙两种方案的改良。为了检查甲、乙两种方案的改良效果，随机在这两种方案中各任意抽取了40件产品作为样本逐件称出它们的重量（单位：克），重量值落在
之间的产品为合格品，否则为不合格品。下表是甲、乙两种方案样本频数分布表。
产品重量 | 甲方案频数 | 乙方案频数 |
| 6 | 2 |
| 8 | 12 |
| 14 | 18 |
| 8 | 6 |
| 4 | 2 |
（1）根据上表数据求甲(同组中的重量值用组中点数值代替)方案样本中40件产品的平均数和中位数
（2）由以上统计数据完成下面
列联表，并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
甲方案 | 乙方案 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
参考公式：
，其中
.
临界值表：
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.814 | 5.024 | 6.635 | 10.828 |
