题目内容
6.已知数列{an}满足,an+1+an=2n.(1)当a1=$\frac{1}{2}$时,求数列{an}的前n项和Sn;
(2)若对任意n∈N*,都有$\frac{{{a}_{n}}^{2}+{{a}_{n+1}}^{2}}{{a}_{n}+{a}_{n+1}}$≥4成立,求a1的取值范围.
分析 (1)当n为偶数时,S=(a1+a2)+(a3+a4)+…+(an-1+an),当n是奇数时,S=a1+(a2+a3)+(a4+a5)+…+(an-1+an),然后由等差数列的前n项和得答案;
(2)由递推式得出an+2-an=2,可判断奇数项和偶数项分别构成等差数列,公差为2,当n为奇数时,an=a1+n-1,an+1=n+1-a1,得出${{a}_{1}}^{2}-2{a}_{1}≥-{n}^{2}+4n-1$,构造函数求最值求解;当n为偶数时,an=n-a1,an+1=n+a1,得出${{a}_{1}}^{2}≥-{n}^{2}+4n$,构造函数求最值求解,最后对a1的范围取并集得答案.
解答 解:(1)由an+1+an=2n,
当n为奇数时,Sn=a1+(a2+a3)+(a4+a5)+…+(an-1+an)
=$\frac{1}{2}+2[2+4+…+(n-1)]$=$\frac{1}{2}+2×\frac{(2+n-1)×\frac{n-1}{2}}{2}=\frac{{n}^{2}}{2}$;
当n为偶数时,Sn=(a1+a2)+(a3+a4)+…+(an-1+an)
=2[1+3+…+(n-1)]=2×$\frac{(1+n-1)×\frac{n-1}{2}}{2}$=$\frac{{n}^{2}-n}{2}$.
∴${S}_{n}=\left\{\begin{array}{l}{\frac{{n}^{2}}{2},n为奇数}\\{\frac{{n}^{2}-n}{2},n为偶数}\end{array}\right.$;
(2)由an+1+an=2n,得an+2+an+1=2(n+1),
∴an+2-an=2,则数列{an}的奇数项和偶数项分别构成以2为公差的等差数列.
当n为奇数时,an=n-1+a1,an+1=n+1-a1,
∵$\frac{{{a}_{n}}^{2}+{{a}_{n+1}}^{2}}{{a}_{n}+{a}_{n+1}}$≥4,∴${{a}_{1}}^{2}-2{a}_{1}≥-{n}^{2}+4n-1$.
令f(n)=-n2+4n-1,∴f(n)max=3,
由${{a}_{1}}^{2}-2{a}_{1}≥3$,解得a1≤-1或a1≥3;
当n为偶数时,an=n-a1,an+1=n+a1,
∵$\frac{{{a}_{n}}^{2}+{{a}_{n+1}}^{2}}{{a}_{n}+{a}_{n+1}}$≥4,∴${{a}_{1}}^{2}≥-{n}^{2}+4n$.
令g(n)=-n2+4n,∴g(n)max=4,
由${{a}_{1}}^{2}≥4$,解得a1≤-2或a1≥2.
综上,a1的范围是(-∞,-1)∪(2,+∞).
点评 本题综合考查数列与函数,等差数列的通项公式,考查分类讨论思想、整体思想的运用,属于难题.

| A. | [2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$](k∈Z) | B. | [$\frac{kπ}{2}$-$\frac{π}{8}$,$\frac{kπ}{2}$+$\frac{π}{8}$](k∈Z) | ||
| C. | [kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$](k∈Z) | D. | [$\frac{kπ}{2}$,$\frac{kπ}{2}$+$\frac{π}{4}$](k∈Z) |
| A. | 14个 | B. | 15个 | C. | 16个 | D. | 17个 |
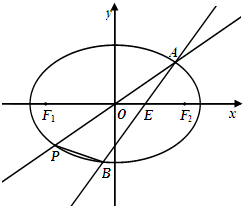 如图,在平面直角坐标系xoy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.
如图,在平面直角坐标系xoy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\frac{{2\sqrt{6}}}{3}$.