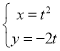题目内容
【题目】某家具厂有方木料
，五合板
，准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
、五合板
；生产每个书橱需要方木枓
、五合板
.出售一张书桌可获利润
元，出售一个书橱可获利润
元，怎样安排生产可使所得利润最大？最大利润为多少？
【答案】生产书桌
张，书橱
个，可使所得利润最大，最大利润为
元.
【解析】【试题分析】本题旨在考查线性规划的知识在解决实际问题中的运用，求解时充分借助题设条件，将问题转化为二元一次不等式组，然后画出不等式组表示的区域，然后数形结合求解：
解：
设生产书桌
张，书橱
个，利润总额为
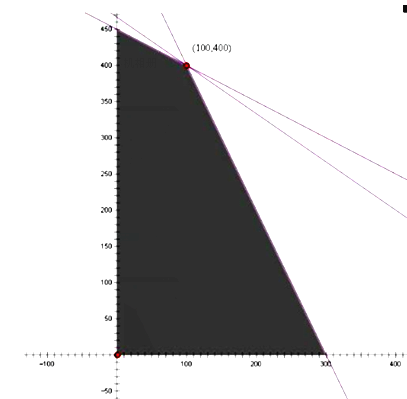
元.则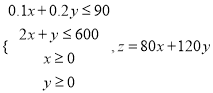
，可行域如图.由图可知：当直线
经过可行域上的点
时，截距
最大，即
最大，解方程组
得
的坐标为
， 
（元）.因此，生产书桌
张，书橱
个，可使所得利润最大，最大利润为
元.
【题目】2017年某市街头开始兴起“mobike”、“ofo”等共享单车，这样的共享单车为很多市民解决了最后一公里的出行难题．然而，这种模式也遇到了一些让人尴尬的问题，比如乱停乱放，或将共享单车占为“私有”等．为此，某机构就是否支持发展共享单车随机调查了50人，他们年龄的分布及支持发展共享单车的人数统计如下表：
年龄 |
|
|
|
|
|
|
受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
支持发展共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
（Ⅰ）由以上统计数据填写下面的
列联表，并判断能否在犯错误的概率不超过0.1的前提下，认为年龄与是否支持发展共享单车有关系：
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | |||
不支持 | |||
合计 |
（Ⅱ）若对年龄在
的被调查人中随机选取两人，对年龄在
的被调查人中随机选取一人进行调查，求选中的3人中支持发展共享单车的人数为2人的概率．
参考数据：
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式：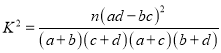 
，其中
．
