题目内容
数列
,-
,
,-
,…的一个通项公式是( )
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 27 |
| 7 |
| 81 |
A.an=(-1)n+1
| B.an=(-1)n
| ||||
C.an=(-1)n+1
| D.an=(-1)n+1
|
将数列的第2项还原为未约分的形式,可得
,-
,
,-
,…
记数列{cn}为1,3,5,7,….可得{cn}构成以1为首项、公差d=2的等差数列,
∴cn=1+2(n-1)=2n-1.
再记数列{bn}为3,-9,27,-81,….可得{bn}构成以3为首项、公比q=-3的等比数列,
∴bn=3×(-3)n-1=(-1)n-1•3n.
∵数列
,-
,
,-
,…的通项公式为an=
的形式,
∴所求通项公式为an=
=(-1)n+1
.
故选:A
| 1 |
| 3 |
| 3 |
| 9 |
| 5 |
| 27 |
| 7 |
| 81 |
记数列{cn}为1,3,5,7,….可得{cn}构成以1为首项、公差d=2的等差数列,
∴cn=1+2(n-1)=2n-1.
再记数列{bn}为3,-9,27,-81,….可得{bn}构成以3为首项、公比q=-3的等比数列,
∴bn=3×(-3)n-1=(-1)n-1•3n.
∵数列
| 1 |
| 3 |
| 3 |
| 9 |
| 5 |
| 27 |
| 7 |
| 81 |
| cn |
| bn |
∴所求通项公式为an=
| 2n-1 |
| (-1)n-1•3n |
| 2n-1 |
| 3n |
故选:A

练习册系列答案
相关题目
 中,
中, ,求
,求 ,并归纳出
,并归纳出 .
. ,
,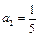 ,且a1a2+a2a3+…+anan+1=na1an+1对于任何正整数n都成立,则
,且a1a2+a2a3+…+anan+1=na1an+1对于任何正整数n都成立,则 的值为 ( )
的值为 ( )


 ”是“
”是“ ”的( )
”的( )