Question

【题目】已知函数，其中常数.

（1）令，将函数的图像向左平移个单位，再向上平移1个单位，得到函数，求函数的解析式；

（2）若在上单调递增，求的取值范围；

（3）在（1）的条件下的函数的图像，区间且满足：在上至少含有30个零点，在所有满足上述条件的中，求的最小值.

Answer 1

【答案】（1）；（2）；（3）

【解析】

（1）根据正弦函数平移“左加右减、上加下减”的法则即可求得；

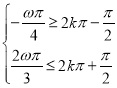（2）利用范围可求得的范围，根据单调性可得不等式组，解不等式组求得；由可求得，两个范围取交集得到最终结果；

（3）令可求得零点，进而得到相邻零点之间的距离；若最小，知均为零点，此时在恰有个零点，从而得到在至少有一个零点；根据相邻零点之间距离即可得到满足的条件，进而求得所求的最小值.

（1）

，即

（2） 当时，

，，解得：，

又

即的取值范围为

（3）令得：

或，

解得：或，

相邻两个零点之间的距离为或

若最小，则均为的零点，此时在区间，，…，分别恰有个零点

在区间恰有个零点 至少有一个零点

，即

检验可知，在恰有个零点，满足题意

的最小值为