题目内容
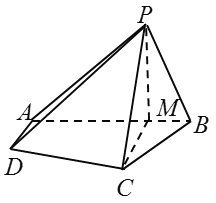
【题目】如图,已知![]() 为椭圆
为椭圆![]() :
: ![]() 的右焦点,
的右焦点, ![]() ,
, ![]() ,
, ![]() 为椭圆的下、上、右三个顶点,
为椭圆的下、上、右三个顶点, ![]() 与
与![]() 的面积之比为
的面积之比为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试探究在椭圆![]() 上是否存在不同于点
上是否存在不同于点![]() ,
, ![]() 的一点
的一点![]() 满足下列条件:点
满足下列条件:点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,
, ![]() 的中点为
的中点为![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,
, ![]() 的中点为
的中点为![]() ,且
,且![]() 的面积为
的面积为![]() .若不存在,请说明理由;若存在,求出点
.若不存在,请说明理由;若存在,求出点![]() 的坐标.
的坐标.
【答案】(1) ![]() .(2)存在满足条件的点
.(2)存在满足条件的点![]() ,其坐标为
,其坐标为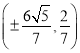 .
.
【解析】试题分析:
(1)由![]() 与
与![]() 的面积之比为
的面积之比为![]() 可得
可得![]() ,又
,又![]() ,所以
,所以![]() ,从而
,从而![]() ,可得椭圆的标准方程。(2)假设存在满足条件的点
,可得椭圆的标准方程。(2)假设存在满足条件的点![]() (
(![]() ),进而
),进而![]() ,
, ![]() 。可得直线
。可得直线![]() 的方程为
的方程为![]() ,进一步可得
,进一步可得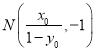 ,根据
,根据![]() ,可得
,可得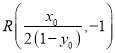 ,从而得到
,从而得到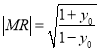 。又点
。又点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,由
,由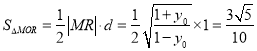 ,可得
,可得![]() ,从而
,从而![]() 。因此存在点P满足条件。
。因此存在点P满足条件。
试题解析:
(1)由已知得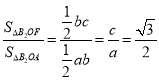 .
.
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)假设存在满足条件的点P,设其坐标为![]() (
(![]() ),
),
则![]() ,且
,且![]() .
.
又![]() ,
,
∴直线![]() 的方程为
的方程为![]() .
.
∵![]() ,∴
,∴![]() ,
,
令![]() ,得
,得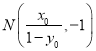 .
.
又![]() ,则
,则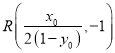 ,
,
∴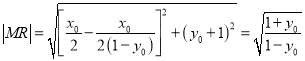 .
.
直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
∴点![]() 到直线
到直线![]() 的距离为
的距离为 ,
,
∴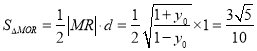 ,
,
解得![]() ,
,
又![]() ,
,
∴![]() ,
,
∴存在满足条件的点![]() ,其坐标为
,其坐标为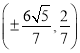 .
.

【题目】某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下:
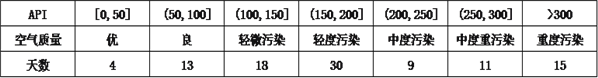
记某企业每天由空气污染造成的经济损失T(单位:元),空气质量指数API为![]() .在区间[0,100]对企业没有造成经济损失;在区间(100,300]对企业造成经济损失成直线模型(当API为150时造成的经济损失为200元,当API为200时,造成的经济损失为400元);当API大于300时造成的经济损失为2000元.
.在区间[0,100]对企业没有造成经济损失;在区间(100,300]对企业造成经济损失成直线模型(当API为150时造成的经济损失为200元,当API为200时,造成的经济损失为400元);当API大于300时造成的经济损失为2000元.
(1)试写出函数T(![]() )的表达式:
)的表达式:
(2)试估计在本年内随机抽取一天,该天经济损失大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关.
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
附: 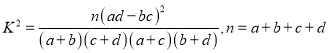
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】近年来许多地市空气污染较为严重,现随机抽取某市一年(365天)内100天的![]() 空气质量指数(
空气质量指数(![]() )的监测数据,统计结果如表:
)的监测数据,统计结果如表:
|
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
天数 | 4 | 13 | 18 | 30 | 20 | 15 |
记某企业每天由空气污染造成的经济损失为![]() (单位:元),
(单位:元),![]() 指数为
指数为.当
![]() 在区间
在区间![]() 内时,对企业没有造成经济损失;当
内时,对企业没有造成经济损失;当![]() 在区间
在区间![]() 内时,对企业造成的经济损失与
内时,对企业造成的经济损失与![]() 成直线模型(当
成直线模型(当![]() 指数为150时,造成的经济损失为1100元,当
指数为150时,造成的经济损失为1100元,当![]() 指数为200时,造成的经济损失为1400元);当
指数为200时,造成的经济损失为1400元);当![]() 指数大于300时,造成的经济损失为2000元.
指数大于300时,造成的经济损失为2000元.
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取1天,该天经济损失![]() 大于1100且不超过1700元的概率;
大于1100且不超过1700元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,这30天中有8天为严重污染,完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该市本年度空气严重污染与供暖有关?
的把握认为该市本年度空气严重污染与供暖有关?
非严重污染 | 严重污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 |
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
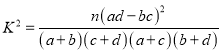 ,其中
,其中![]()