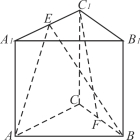
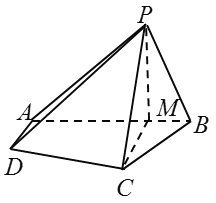
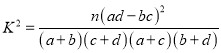题目内容
【题目】在四棱锥
中， 
， 
，点M是线段AB上的一点，且
．
（1）证明：平面
平面ABCD；
（2）求直线CM与平面PCD所成角的正弦值．
【答案】（1）见解析（2）
【解析】试题分析：(1)由长度关系，可证
，再由PM
平面ABCD，从而证明平面
平面ABCD。（2）通过M点做CD的垂面PMH，进而做出面PCD的垂线MN,线面角为
。
试题解析：（1）由
，得
，
又因为
，且AB与CD是梯形的两腰，必相交，所以PM
平面ABCD ，
且
．所以，平面
平面ABCD。
（2）过点M作
，连结HP，因为
，且
，
所以
，又由
平面PCD
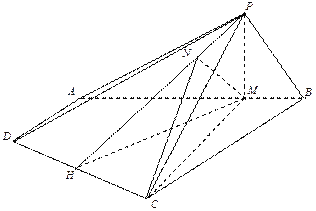
所以平面
，平面
，过点M作
，即有
，所以
为直线CM面PCD所成角．
在四棱锥P-ABCD中，设AB=2t，则CM= 
,PM= 
, 
，
从面
，即直线CM与平面 PCD所成角的正弦值为 
．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
