Question

【题目】已知函数， ．

（Ⅰ）求曲线在处的切线方程．

（Ⅱ）求的单调区间．

（Ⅲ）设，其中，证明：函数仅有一个零点．

Answer 1

【答案】（Ⅰ）（Ⅱ）单调增区间为单调减区间为（Ⅲ）见解析

【解析】试题分析：（Ⅰ）求导，所以，又可得在处的切线方程（Ⅱ）令，解出，令，解出，可得的单调区间．（Ⅲ） ，

在单调递增在单调递减，在单调递增，且极大值， 极小值可得在无零点，

在有一个零点，所以有且仅有一个零点．

试题解析：

（Ⅰ）∵， ，

∴． ，

∴在处切线为，即为．

（Ⅱ）令，解出，

令，解出．

∴的单调增区间为，

单调减区间为．

（Ⅲ）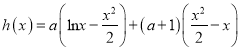

，

．

令，解出或，

令，解出．

∴在单调递增在单调递减，

在单调递增．

极大值，

极小值，

∵在时， 极大值小于零，

在时， 极小值小于零．

在， 单调递增，

说明在无零点，

在有一个零点，

∴有且仅有一个零点．