题目内容
【题目】已知![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 单调递增区间;
单调递增区间;
(2)求证:对任意![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线恒过定点;
处的切线恒过定点;
(3)是否存在实数![]() 的值,使得
的值,使得![]() 在
在![]() 上有最大值或最小值,若存在,求出实数
上有最大值或最小值,若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 或
或![]() .
.
【解析】
试题(1)先求函数导数,再解导函数大于零时解集得函数![]() 单调递增区间,注意两个增区间不可用“或” 、“并”连接,(2)以算代证:先根据导数几何意义求切线斜率,再根据点斜式写切线方程,并按实数
单调递增区间,注意两个增区间不可用“或” 、“并”连接,(2)以算代证:先根据导数几何意义求切线斜率,再根据点斜式写切线方程,并按实数![]() 整理,最后根据恒成立列关于
整理,最后根据恒成立列关于![]() 的方程组,解出定点坐标,(3)先求函数导数,再研究导函数零点,即转化为研究一元二次方程实根分布:没有实根或有两个相同实根时,导函数不变号,函数为单调递增函数,值域为
的方程组,解出定点坐标,(3)先求函数导数,再研究导函数零点,即转化为研究一元二次方程实根分布:没有实根或有两个相同实根时,导函数不变号,函数为单调递增函数,值域为![]() ,没有最值;有两个不同实根时,函数先增后减再增,只需极小值非正, 就可取到最小值,解不等式可得实数
,没有最值;有两个不同实根时,函数先增后减再增,只需极小值非正, 就可取到最小值,解不等式可得实数![]() 的取值范围.
的取值范围.
试题解析:(1)当![]() 时,
时,![]() ,
,![]() .
.
令![]() ,得
,得![]() 或
或![]() .
.
∴函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() .
.
(2)![]() ,
,
![]() ,
,![]() .
.
∴函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() .
.
即![]() .
.
方程![]() 可化为
可化为![]() ,
,
当![]() 即
即![]() 时,对任意
时,对任意![]() ,
,![]() 恒成立.
恒成立.
∴函数![]() 的图象在
的图象在![]() 点处的切线方程
点处的切线方程![]() 经过定点
经过定点![]() .
.
(3)![]() .
.
令![]() ,
,![]() ,
,
![]() ,
,![]() .
.
①当![]() 即
即![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上不存在最大值和最小值.
上不存在最大值和最小值.
②当![]() 即
即![]() 或
或![]() 时,设方程
时,设方程![]() 的两根为
的两根为![]() .
.
![]() 随
随![]() 的变化情况如下表:
的变化情况如下表:

当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() .
.
∴要使![]() 在
在![]() 上有最大值或最小值,只需满足
上有最大值或最小值,只需满足![]() 即
即![]() 有解.
有解.
∴![]() ,解得
,解得![]() 或
或![]() .
.
综上可得,![]() 或
或![]() .
.

【题目】已知某蔬菜商店买进的土豆![]() (吨)与出售天数
(吨)与出售天数![]() (天)之间的关系如下表所示:
(天)之间的关系如下表所示:
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(1)请根据上表数据在下列网格纸中绘制散点图;
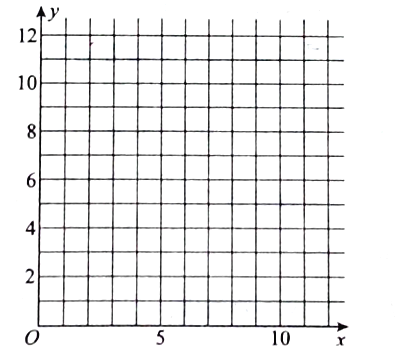
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (其中
(其中![]() 保留三位小数);(注:
保留三位小数);(注: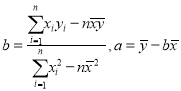 )
)
(3)在表格中(![]() 的8个对应点中,任取3个点,记这3个点在直线
的8个对应点中,任取3个点,记这3个点在直线![]() 的下方的个数为
的下方的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.