题目内容
【题目】已知某蔬菜商店买进的土豆![]() (吨)与出售天数
(吨)与出售天数![]() (天)之间的关系如下表所示:
(天)之间的关系如下表所示:
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
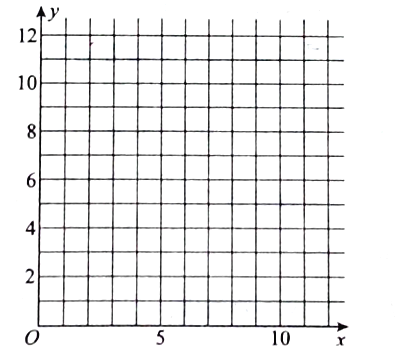
(1)请根据上表数据在下列网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (其中
(其中![]() 保留三位小数);(注:
保留三位小数);(注: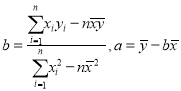 )
)
(3)在表格中(![]() 的8个对应点中,任取3个点,记这3个点在直线
的8个对应点中,任取3个点,记这3个点在直线![]() 的下方的个数为
的下方的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)见解析(2)![]() (3)见解析
(3)见解析
【解析】
试题(1)根据所给数据画出散点图即可;(2)根据最小二乘法,利用公式求出求出![]() ,将中心点的坐标带入,求出回归方程中的系数,即可得结果;(3)
,将中心点的坐标带入,求出回归方程中的系数,即可得结果;(3)![]() 的可能取值为0,1,2,3,分别求出各随机变量的概率,从而可得分布列,由期望公式可得结果.
的可能取值为0,1,2,3,分别求出各随机变量的概率,从而可得分布列,由期望公式可得结果.
试题解析:(1)散点图如下所示:
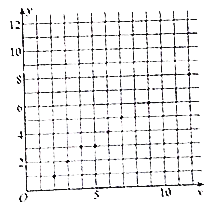
(2)依题意,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
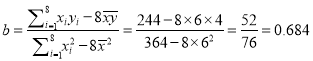 ,
,
∴![]() ;
;
∴回归直线方程为![]() (注:
(注:![]() 也可)
也可)
(3)在![]() 对应的8个点中,有4个点在直线
对应的8个点中,有4个点在直线![]() 的下方,所以
的下方,所以![]() 的可能取值为0,1,2,3,
的可能取值为0,1,2,3,
![]() ,
,
∴![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() 的数学期望
的数学期望![]() .
.
【方法点晴】本题主要考查散点图的画法和线性回归方程,以及离散型随机变量的期望,属于中档题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ;(2) 回归直线过样本点中心
;(2) 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目