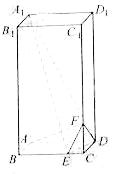
题目内容
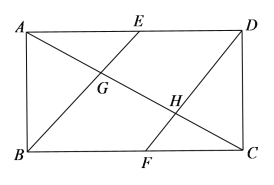
【题目】如图，一张矩形白纸
，
，
，
，
分别为
，
的中点，现分别将
，
沿
，DF折起，且
、
在平面
同侧，下列命题正确的是_________（写出所有正确命题的序号）
①平面
平面
时，
②当平面平面时，
平面
③当、重合于点
时，
④当、重合于点时，三棱锥
的外接球的半径为
【答案】②
【解析】
分别作出平面
平面
时，
、
重合于点
时几何体图形，根据线面位置关系和长度关系证明判定，利用补图法求外接球的半径．
由题：矩形
中，
，
，
，
分别为
，
的中点，
，
所以
，同理可得
，
，
，
中，
，所以
，
由余弦定理
，
当平面平面时，如图：
所以在折叠后的图形中
，
，
可得
平面
，
平面
，由于，
平面与平面都经过
，则平面与平面重合，
所以四边形
为平行四边形，
，
平面
，
平面
所以
平面，所以②正确；
假设
，则四边形
为平行四边形，可得
与
矛盾，所以①矛盾；
当、重合于点时，如图：
由题可得：
，
，
，所以不可能
，所以③错误；
三棱锥
中，
，
所以
为直角三角形，
，
，所以
为直角三角形，
为直角三角形，
由补图法可知三棱锥的与以
为长宽高的长方体外接球相同，
其直径为
，
所以外接球的半径为
，所以④不正确；
故答案为：②
练习册系列答案
同步奥数系列答案
相关题目
