Question

【题目】如图，在三棱柱中，平面.且四边形是菱形，.

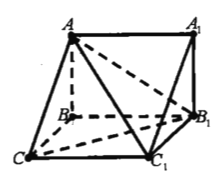
（1）求证：；

（2）若,三棱锥的体积为，求的面积.

Answer 1

【答案】（1）见解析；（2）.

【解析】

试题（1）连结，因为平面，可得.

因为四边形是菱形，可知,然后根据线面垂直的判定定理可得平面.据此即可证明结果；（2）由平面，可知.设菱形的边长为，因为，由余弦定理可得.因为，由勾股定理得，所以.因为平面，可得,所以在中，.因为,可得：，根据，据此即可求出结果.

试题解析：

（1）证明：连结，

因为平面，平面，所以.

因为四边形是菱形，所以,

又因为 ，所以平面.

因为平面，所以.

（2）由平面，可知.

设菱形的边长为，

因为，所以.

因为，所以，所以.

因为平面，侧面，所以,

所以在中，.

因为,

解得：，所以，.

所以.