题目内容
已知圆C的方程是x2+y2-4x-4y-10=0，直线l：y=-x，则圆C上有几个点到直线l的距离为2
（ ）
| 2 |
| A．1个 | B．2个 | C．3个 | D．4个 |
圆C的方程是x2+y2-4x-4y-10=0，
即（x-2）2+（y-2）2=18，圆心为（2，2），r=3
．
又因为（2，2）到直线y=-x的距离d=
=2
＜3
．
所以圆与直线相交，而到直线l的距离为2
的点应在直线两侧，且与已知直线平行的直线上
．
两平行线与圆相交的只有一条．
故满足条件的点只有两个．
故选B．
即（x-2）2+（y-2）2=18，圆心为（2，2），r=3
| 2 |
又因为（2，2）到直线y=-x的距离d=
| |2+2| | ||
|
| 2 |
| 2 |
所以圆与直线相交，而到直线l的距离为2
| 2 |
．两平行线与圆相交的只有一条．
故满足条件的点只有两个．
故选B．
练习册系列答案
阅读快车系列答案
相关题目
、
是方程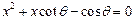
的两个不相等的实数根，那么过点
和点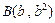
的直线与圆
的位置关系是 
与直线
始终有交点，则
的取值范围是___________；