题目内容
3.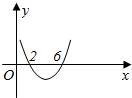 已知函数f(x)=ax(x-c)2在点x=x0处取得极大值32,其导函数y=f′(x)的图象经过点(2,0)、(6,0),如图.
已知函数f(x)=ax(x-c)2在点x=x0处取得极大值32,其导函数y=f′(x)的图象经过点(2,0)、(6,0),如图.(1)求x0的值;
(2)求函数f(x)的解析式.
分析 (1)求函数的导数,y=f′(x)的图象经过点(2,0)、(6,0),求出c的值即可求x0的值;
(2)根据函数的极值,建立方程关系求出a,即可求函数f(x)的解析式.
解答 解:(1)函数的导数f′(x)=a(x-c)2+2ax(x-c)=3a(x-c)(x-$\frac{c}{3}$),
∵y=f′(x)的图象经过点(2,0)、(6,0),
∴2,6是方程f′(x)=0的两个根,且a>0,
则c=6,
则f′(x)=3a(x-6)(x-2),f(x)=ax(x-6)2,
由f′(x)>0得x>6或x<2,此时函数单调递增,
由f′(x)<0得2<x<6,此时函数单调递减,
则当x=2时,函数取得极大值,此时x0=2.
(2)由(1)知当x=2时,函数取得极大值,极大值为32,
即f(2)=2a×16=32,解得a=1,
∴f(x)=x(x-6)2.
点评 本题主要考查函数解析式的求解,求函数的导数,利用函数单调性,极值和导数之间的关系是解决本题的关键.

练习册系列答案
相关题目
13.直线ax+by=1与圆x2+y2=1相交于A,B两点,若△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(2,2)之间距离的最小值为$\sqrt{2}$,最大值3$\sqrt{2}$.
18.海面上有两座灯塔A,B,与观察站C的距离都是m km,灯塔A在观察站C的北偏东40°,灯塔B在观察站C的南偏东20°,则灯塔A,B间的距离是( )
| A. | m km | B. | $\sqrt{2}m\\;km$ km | C. | 2m km | D. | $\sqrt{3}m$ km |