题目内容
13.(1)已知函数f(x)=-x2+2x+3.若x∈[a,a+1](a∈R),请问函数f(x)是否存在最大(小)值?若存在,请求出相应的最值;若不存在,请说明理由.(2)己知函数f(x)=-x2+ax+3.若x∈[2,4](a∈R),请问函数f(x)是否存在最大(小)值?若存在,请求出相应的最值;若不存在,请说明理由.
分析 (1)求出对称轴x=1,讨论[a,a+1]和对称轴的关系,结合单调性即可得到最值;
(2)求得对称轴x=$\frac{a}{2}$,讨论区间[2,4]与对称轴的关系,由单调性即可得到所求最值.
解答 解:(1)函数f(x)=-x2+2x+3的对称轴为x=1,
当a>1时,区间[a,a+1]为减区间,
即有f(a)=-a2+2a+3,为最大值,
f(a+1)=4-a2,为最小值;
当a+1<1即a<0,区间[a,a+1]为增区间,
即有f(a)=-a2+2a+3,为最小值,
f(a+1)=4-a2,为最大值;
当a≤1≤a+1,即0≤a≤1时,f(1)=4为最大值,
f(x)的最小值为f(a)、f(a+1)中较小的一个.
(2)函数f(x)=-x2+ax+3的对称轴为x=$\frac{a}{2}$,
当$\frac{a}{2}$<2即a<4时,[2,4]为减区间,
即有f(2)=2a-1为最大值,f(4)=4a-13为最小值;
当$\frac{a}{2}$>4即a>8时,[2,4]为增区间,
即有f(2)=2a-1为最小值,f(4)=4a-13为最大值;
当2≤$\frac{a}{2}$≤4即4≤a≤8时,f($\frac{a}{2}$)=3+$\frac{{a}^{2}}{4}$为最大值,
最小值为f(2),f(4)中较小的一个.
点评 本题考查二次函数的最值的求法,考查定区间和动轴,以及动区间和定轴的关系,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
1.函数f(x)是定义在R上的函数,且f(x)在区间(0,2)上为增函数,对于任意x∈R,都有f(x)=f(4-x),则( )
| A. | f(1)<f($\frac{5}{2}$)<f($\frac{7}{2}$) | B. | f($\frac{5}{2}$)<f(1)<f($\frac{7}{2}$) | C. | f($\frac{7}{2}$)<f(1)<f($\frac{5}{2}$) | D. | f($\frac{7}{2}$)<f($\frac{5}{2}$)<f(1) |
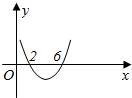 已知函数f(x)=ax(x-c)2在点x=x0处取得极大值32,其导函数y=f′(x)的图象经过点(2,0)、(6,0),如图.
已知函数f(x)=ax(x-c)2在点x=x0处取得极大值32,其导函数y=f′(x)的图象经过点(2,0)、(6,0),如图.