题目内容
11.已知其函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2x(x>0)}\\{0(x=0)}\\{{x}^{2}+mx(x<0)}\end{array}\right.$(1)求实数m的值,并画出y=f(x)的图象
(2)若函数f(x)的图象向右平移1,得到函数y=g(x)的图象,而且函数y=g(x)在区间[0,|a|-2]上单凋递增,试求出函数y=g(x)的解析式并确定a的取值范围.
分析 (1)根据奇函数的性质求出m的值;
(2)根据图象的平移得到函数g(x)的解析式,借助于二次函数的图象,分析得到区间右端点的范围,解绝对值得不等式得到a的取值范围
解答  解:(1)函数f(x)为奇函数,故f(-x)=f(x),
解:(1)函数f(x)为奇函数,故f(-x)=f(x),
设x<0,则-x>0,
∴f(-x)=-(-x)2-2x=-x2-2x=-f(x),
∴f(x)=x2+2x=x2+mx,
∴m=2,
∴f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2x,x>0}\\{0,x=0}\\{{x}^{2}+2x,x<0}\end{array}\right.$,
其图象如右图所示:
(2)函数f(x)的图象向右平移1,得到函数y=g(x)的图象,
∴g(x)=f(x-1)=$\left\{\begin{array}{l}{-{x}^{2}+4x-3,x>1}\\{{x}^{2}-1,x≤1}\end{array}\right.$画出函数g(x)的图象,如下图,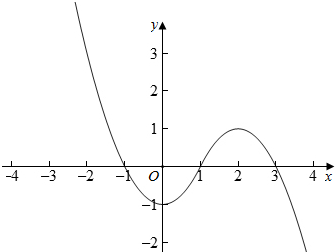
由图象可知,g(x)在[-1,2]上单调递增,要使f(x)在区间[0,|a|-2]上单调递增,
则只需:0<|a|-2≤2,解得-4≤a<0,或0<a≤4,
∴a的取值范围是:[-4,0)∪(0,4].
点评 本题考查了二次函数的图象,考查了二次函数的性质,数形结合有助于我们的解题,形象直观,此题是中档题.

练习册系列答案
相关题目
1.函数f(x)是定义在R上的函数,且f(x)在区间(0,2)上为增函数,对于任意x∈R,都有f(x)=f(4-x),则( )
| A. | f(1)<f($\frac{5}{2}$)<f($\frac{7}{2}$) | B. | f($\frac{5}{2}$)<f(1)<f($\frac{7}{2}$) | C. | f($\frac{7}{2}$)<f(1)<f($\frac{5}{2}$) | D. | f($\frac{7}{2}$)<f($\frac{5}{2}$)<f(1) |
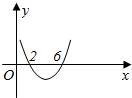 已知函数f(x)=ax(x-c)2在点x=x0处取得极大值32,其导函数y=f′(x)的图象经过点(2,0)、(6,0),如图.
已知函数f(x)=ax(x-c)2在点x=x0处取得极大值32,其导函数y=f′(x)的图象经过点(2,0)、(6,0),如图.