题目内容
【题目】已知![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,
, ![]() ,
, ![]() 为函数
为函数![]() 的两个零点,求证:
的两个零点,求证: ![]() .
.
【答案】(Ⅰ)见解析; (Ⅱ)见解析.
【解析】试题分析: (Ⅰ)根据导数![]() ,分类讨论,当
,分类讨论,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, 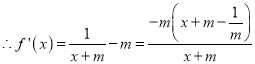 ,由
,由![]()
得![]() ,
, ![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,即可得出单调区间;(Ⅱ)由(Ⅰ)知
,即可得出单调区间;(Ⅱ)由(Ⅰ)知![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .不妨设
.不妨设![]() ,由条件知
,由条件知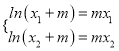 ,即
,即![]() ,构造函数
,构造函数![]() ,
, ![]() 与
与![]() 图像两交点的横坐标为
图像两交点的横坐标为![]() ,
, ![]() ,利用单调性只需证
,利用单调性只需证![]()
构造函数利用单调性证明.
试题解析:(Ⅰ) ![]() ,
, ![]()
当![]() 时,
时, ![]() ,即
,即![]() 的单调递增区间为
的单调递增区间为![]() ,无减区间;
,无减区间;
当![]() 时,
时, 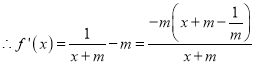 ,由
,由![]()
得![]()
![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
![]() 时,易知
时,易知![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]()
(Ⅱ)由(Ⅰ)知![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
不妨设![]() ,由条件知
,由条件知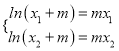 ,即
,即![]()
构造函数![]() ,
, ![]() 与
与![]() 图像两交点的横坐标为
图像两交点的横坐标为![]() ,
, ![]()
由![]() 可得
可得![]() ,
,
而![]() ,
, ![]()
知![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
可知![]()
欲证![]() ,只需证
,只需证![]() ,即证
,即证![]()
考虑到![]() 在
在![]() 上递增,只需证
上递增,只需证![]()
由![]() 知,只需证
知,只需证![]()
令![]() ,
,
则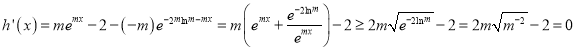
即![]() 单增,又
单增,又![]() ,
,
结合![]() 知
知![]() ,即
,即![]() 成立,
成立,
即![]() 成立
成立

练习册系列答案
相关题目

