题目内容
【题目】已知曲线C1，C2的极坐标方程分别为ρ＝2cosθ， 
，射线θ＝φ， 
， 
与曲线C1交于（不包括极点O）三点A，B，C．
（Ⅰ）求证： 
；
（Ⅱ）当
时，求点B到曲线C2上的点的距离的最小值．
【答案】(I)证明见解析；（Ⅱ） 
.
【解析】试题分析：（Ⅰ）将
， 
代入曲线
的极坐标方程可得
， 
，然后利用两角和与差的余弦公式及三角函数的有界性可得结果；（Ⅱ）曲线C2的直角坐标方程为
，B的直角坐标为（
， 
），根据点到直线距离公式可得结果.
试题解析：（Ⅰ）依题意｜OA｜＝2cosφ， 
， 
，
则
＝4cosφcos
＝
．
（Ⅱ）解：∵
，
∴
，
曲线C2的直角坐标方程为
．
又∵B的极坐标为（1， 
），化为直角坐标为（
， 
），
∴B到曲线C2的距离为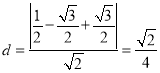
，
∴所求距离的最小值为
．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
