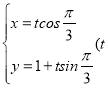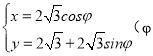题目内容
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为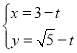 (
(![]() 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的方程
的方程![]() ,
,
(1)求直线![]() 和圆
和圆![]() 的直角坐标方程;
的直角坐标方程;
(3)设圆![]() 与直线
与直线![]() 交于点
交于点![]() 、
、![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() ,
,
【答案】(1)直线![]() :
:![]() ,圆
,圆![]() :
:![]() (2)
(2)![]()
【解析】
(1)因为直线![]() 的参数方程为
的参数方程为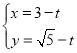 (
(![]() 为参数),消掉参数
为参数),消掉参数![]() ,即可得到直线
,即可得到直线![]() 直角坐标方程.因为圆
直角坐标方程.因为圆![]() 的方程
的方程![]() ,利用极坐标化直角坐标的公式:
,利用极坐标化直角坐标的公式:![]() ,即可求得答案.
,即可求得答案.
(2)将直线![]() 的参数方程化为:
的参数方程化为: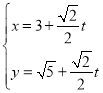 和圆
和圆![]() 的直角坐标方程建立方程组,利用韦达定理,即可求得答案.
的直角坐标方程建立方程组,利用韦达定理,即可求得答案.
(1)![]() 直线
直线![]() 的参数方程为
的参数方程为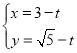 (
(![]() 为参数),
为参数),
消掉![]() 得:
得:![]()
即:![]()
![]() 圆的极坐标方程:
圆的极坐标方程:![]() ,
,
转化为:![]() .
.
即:![]()
![]() 直线
直线![]() 直角坐标方程为:
直角坐标方程为:![]() ,圆
,圆![]() 的直角坐标方程:
的直角坐标方程:![]()
(2)将直线![]() 的参数方程化为:
的参数方程化为: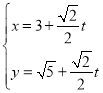 (
(![]() 参数)
参数)
代入圆的直角坐标方程得: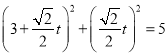
![]()
根据韦达定理可得: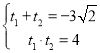
可得![]()
根据直线标准参数方程的参数几何意义可得:
![]()
![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】学校组织高考组考工作,为了搞好接待组委会招募了![]() 名男志愿者和
名男志愿者和![]() 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有![]() 人和
人和![]() 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
(1)根据以上数据完成以下![]() 列联表;并要求列联表的独立性检验,能否在犯错误的概率不超过
列联表;并要求列联表的独立性检验,能否在犯错误的概率不超过![]() 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?
喜爱运动 | 不喜爱运动 | 总计 | |
男 |
|
| |
女 |
|
| |
总计 |
|
(2)如果从喜欢运动的女志愿者中(其中恰有![]() 人会外语),抽取
人会外语),抽取![]() 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中![]() 人恰有一人胜任翻译工作的概率是多少?
人恰有一人胜任翻译工作的概率是多少?
参考公式: ,其中
,其中![]() .
.
参考答数:
|
|
|
|
|
|
|
|
|
|