题目内容
设m、n是两条不同的直线, 是两个不同的平面,则下列命题中正确的是
是两个不同的平面,则下列命题中正确的是
A.若m∥n,m  ,则n∥ ,则n∥ ; ; | B.若 ⊥β,m∥ ⊥β,m∥ ,则m⊥β; ,则m⊥β; |
C.若 ⊥β,m⊥β,则m∥ ⊥β,m⊥β,则m∥ ; ; | D.若m⊥n,m⊥ ,n⊥β,则 ,n⊥β,则 ⊥β ⊥β |
D
解析试题分析:A不正确,m∥n,m?α,由于n可能在α内,故推不出n∥α;
对于B,由于当满足 ⊥β,m∥
⊥β,m∥ ,则m与β可能斜交,因此错误
,则m与β可能斜交,因此错误
对于C,由于; ⊥β,m⊥β,则m∥
⊥β,m⊥β,则m∥ ,也可能m在
,也可能m在 内,错误
内,错误
对于D,则根据m⊥n,m⊥ ,n⊥β,则
,n⊥β,则 ⊥β,符合面面垂直的判定定理,成立,故选D.
⊥β,符合面面垂直的判定定理,成立,故选D.
考点:空间中线面和面民的平行垂直关系
点评:本题考查线面,线线、面面的平行关系的判断,重点考查了空间的感知能力与空间中线面之间位置关系的判断能力.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知直线 ,平面
,平面 ,且
,且 ,给出四个命题: ①若
,给出四个命题: ①若 ∥
∥ ,则
,则 ;②若
;②若 ,则
,则 ∥
∥ ;③若
;③若 ,则
,则 ∥m;④若
∥m;④若 ∥m,则
∥m,则 .其中真命题的个数是
.其中真命题的个数是
| A.4 | B.3 | C.2 | D.1 |
从正方体的八个顶点中任取四个点连线,在能构成的一对异面直线中,其所成的角的度数不可能是
| A.30° | B.45° | C.60° | D.90° |
已知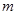 、
、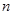 为两条不同的直线,
为两条不同的直线,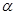 、
、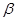 为两个不同的平面,则下列推理中正确的是( )
为两个不同的平面,则下列推理中正确的是( )
A.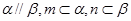 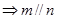 | B.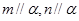 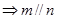 |
C.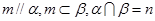 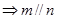 | D.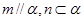 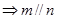 |
已知m、n是两条不同的直线, 、
、 、
、 是三个不同的平面,下列命题中错误的是( )
是三个不同的平面,下列命题中错误的是( )
A.若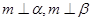 则 则 ∥ ∥ |
B.若 ∥ ∥ , , ∥ ∥ 则 则 ∥ ∥ |
C.若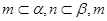 ∥n则 ∥n则 ∥ ∥ |
D.若m、n是异面直线,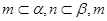 ∥ ∥ ,n∥ ,n∥ 则 则 ∥ ∥ |
设 ,
, 是两条不同的直线,
是两条不同的直线,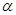 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
如果对于空间任意n(n≥2)条直线总存在一个平面α,使得这n条直线与平面α所成的角均相等,那么这样的n( )
| A.最大值为3 | B.最大值为4 | C.最大值为5 | D.不存在最大值 |
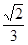
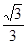
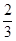
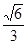
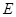 是
是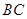 的中点,P点在侧面△SCD内及其边界上运动,并且总是保持
的中点,P点在侧面△SCD内及其边界上运动,并且总是保持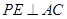 .则动点
.则动点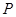 的轨迹与△
的轨迹与△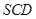 组成的相关图形最有可有是图中的( )
组成的相关图形最有可有是图中的( )