题目内容
已知在四棱锥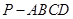 中,底面
中,底面 是矩形,且
是矩形,且 ,
, ,
, 平面
平面 ,
, 、
、 分别是线段
分别是线段 、
、 的中点.
的中点.

(1)证明: ;
;
(2)判断并说明 上是否存在点
上是否存在点 ,使得
,使得 ∥平面
∥平面 ;
;
(3)若 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角 的余弦值.
的余弦值.
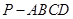 中,底面
中,底面 是矩形,且
是矩形,且 ,
, ,
, 平面
平面 ,
, 、
、 分别是线段
分别是线段 、
、 的中点.
的中点.
(1)证明:
 ;
;(2)判断并说明
 上是否存在点
上是否存在点 ,使得
,使得 ∥平面
∥平面 ;
;(3)若
 与平面
与平面 所成的角为
所成的角为 ,求二面角
,求二面角 的余弦值.
的余弦值.(Ⅰ)略(Ⅱ)满足 的点
的点 即为所求.
即为所求.
(Ⅲ)二面角 的余弦值为
的余弦值为 .
.
 的点
的点 即为所求.
即为所求.(Ⅲ)二面角
 的余弦值为
的余弦值为 .
.本题考查的知识点是用空间向量求平面间的夹角,空间直线与直线之间的位置关系,直线与平面平行的判定,其中解法一的关键是建立的空间坐标系,将空间线面关系转化为向量夹角问题,解法二的关键是熟练掌握空间线面关系的判定,性质.
(I)连接AF,由勾股定理可得DF⊥AF,由PA⊥平面ABCD,由线面垂直性质定理可得DF⊥PA,再由线面垂直的判定定理得到DF⊥平面PAF,再由线面垂直的性质定理得到PF⊥FD;
(Ⅱ)过点E作EH∥FD交AD于点H,则EH∥平面PFD,且有AH=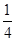
AD,再过点H作HG∥DP交PA于点G,则HG∥平面PFD且AG=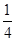
AP,由面面平行的判定定理可得平面GEH∥平面PFD,进而由面面平行的性质得到EG∥平面PFD.从而确定G点位置;(Ⅲ)由PA⊥平面ABCD,可得∠PBA是PB与平面ABCD所成的角,即∠PBA=45°,取AD的中点M,则FM⊥AD,FM⊥平面PAD,在平面PAD中,过M作MN⊥PD于N,连接FN,则PD⊥平面FMN,则∠MNF即为二面角A-PD-F的平面角,解三角形MNF可得答案
(I)连接AF,由勾股定理可得DF⊥AF,由PA⊥平面ABCD,由线面垂直性质定理可得DF⊥PA,再由线面垂直的判定定理得到DF⊥平面PAF,再由线面垂直的性质定理得到PF⊥FD;
(Ⅱ)过点E作EH∥FD交AD于点H,则EH∥平面PFD,且有AH=
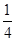
AD,再过点H作HG∥DP交PA于点G,则HG∥平面PFD且AG=
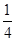
AP,由面面平行的判定定理可得平面GEH∥平面PFD,进而由面面平行的性质得到EG∥平面PFD.从而确定G点位置;(Ⅲ)由PA⊥平面ABCD,可得∠PBA是PB与平面ABCD所成的角,即∠PBA=45°,取AD的中点M,则FM⊥AD,FM⊥平面PAD,在平面PAD中,过M作MN⊥PD于N,连接FN,则PD⊥平面FMN,则∠MNF即为二面角A-PD-F的平面角,解三角形MNF可得答案

练习册系列答案
相关题目
 中,底面
中,底面 为平行四边形
为平行四边形 底面
底面

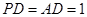 ,求棱锥
,求棱锥 的高.
的高.  的底面为直角梯形,
的底面为直角梯形, ∥
∥ ,∠
,∠ ,
, ⊥底面
⊥底面 ,且
,且 ,
, 是
是 的中点.
的中点.
 ⊥平面
⊥平面 ;
; 与
与 的余弦值.
的余弦值.


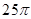
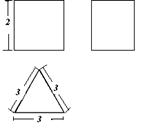

 ,则该几何体的体积为______________;
,则该几何体的体积为______________;
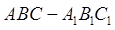 中,
中,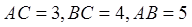 ,
,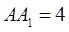 ,点D是AB的中点.
,点D是AB的中点.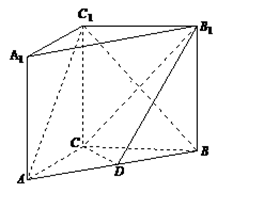
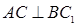 ;
;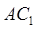 ∥平面
∥平面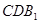 ;
; 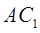 与
与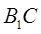 所成角的余弦值.
所成角的余弦值.  中,
中,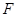 为
为 的中点.
的中点.
 与面
与面 的交线的位置,并说明理由;
的交线的位置,并说明理由; 上确定一点
上确定一点 ,使得面
,使得面 面
面 的正切值.
的正切值.




