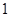题目内容
(本小题满分12分)
已知四棱锥 的底面为直角梯形,
的底面为直角梯形, ∥
∥ ,∠
,∠ ,
, ⊥底面
⊥底面 ,且
,且 ,
, 是
是 的中点.
的中点.

(1)证明:平面 ⊥平面
⊥平面 ;
;
(2)求 与
与 所成角的余弦值;
所成角的余弦值;
(3)求二面角 的余弦值.
的余弦值.
已知四棱锥
 的底面为直角梯形,
的底面为直角梯形, ∥
∥ ,∠
,∠ ,
, ⊥底面
⊥底面 ,且
,且 ,
, 是
是 的中点.
的中点.
(1)证明:平面
 ⊥平面
⊥平面 ;
;(2)求
 与
与 所成角的余弦值;
所成角的余弦值;(3)求二面角
 的余弦值.
的余弦值. (1)见解析;(2) 与
与 所成角的余弦值为
所成角的余弦值为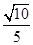 .
.
(3)二面角 的余弦值为
的余弦值为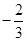 。
。
 与
与 所成角的余弦值为
所成角的余弦值为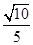 .
.(3)二面角
 的余弦值为
的余弦值为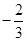 。
。第一问主要考查空间几何体中线,面位置关系的证明!掌握好线面位置关系的判定定理与性质定理注意线线,线面,面面之间的转化有利于证明题的解决。第二三问主要是线线角与二面角的求法。掌握利用向量求空间角的方法。
解:(1)∵ ⊥底面
⊥底面 ,
,
∴ ⊥
⊥
又∠
∴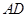 ⊥
⊥
而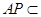 平面
平面 ,
,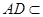 平面
平面 ,
,
且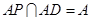
∴ ⊥平面
⊥平面 ,…………2分
,…………2分
又 ∥
∥
∴ ⊥平面
⊥平面 ,…………3分
,…………3分
又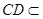 平面
平面 ,
,
∴平面 ⊥平面
⊥平面 . …………………………4分
. …………………………4分
(2)由(1)知可以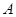 为原点,建立如图空间直角坐标系,
为原点,建立如图空间直角坐标系,
∵ ,
, 是
是 的中点,
的中点,
∴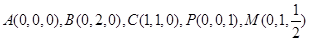 , ………………5分
, ………………5分
∴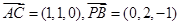 …………………………6分
…………………………6分
∴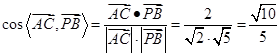 ,
,
∴ 与
与 所成角的余弦值为
所成角的余弦值为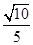 . …………………………8分
. …………………………8分
(3)∵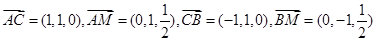
记平面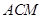 的法向量为
的法向量为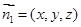
则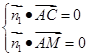 即
即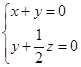 ,令
,令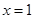 则
则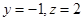 ,
,
∴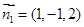 …………………………9分
…………………………9分
同理可得平面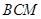 的法向量为
的法向量为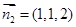 …………………………10分
…………………………10分
∴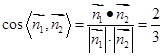 …………………………11分
…………………………11分
又易知二面角 的平面角为钝角,
的平面角为钝角,
∴二面角 的余弦值为
的余弦值为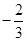 …………………………12分
…………………………12分
解:(1)∵
 ⊥底面
⊥底面 ,
,∴
 ⊥
⊥
又∠

∴
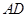 ⊥
⊥
而
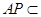 平面
平面 ,
,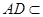 平面
平面 ,
,且
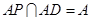
∴
 ⊥平面
⊥平面 ,…………2分
,…………2分又
 ∥
∥
∴
 ⊥平面
⊥平面 ,…………3分
,…………3分又
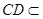 平面
平面 ,
,∴平面
 ⊥平面
⊥平面 . …………………………4分
. …………………………4分(2)由(1)知可以
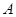 为原点,建立如图空间直角坐标系,
为原点,建立如图空间直角坐标系,∵
 ,
, 是
是 的中点,
的中点,∴
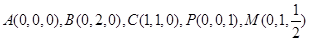 , ………………5分
, ………………5分∴
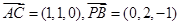 …………………………6分
…………………………6分∴
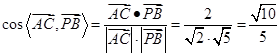 ,
,∴
 与
与 所成角的余弦值为
所成角的余弦值为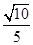 . …………………………8分
. …………………………8分(3)∵
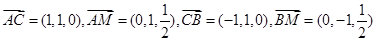
记平面
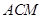 的法向量为
的法向量为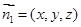
则
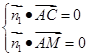 即
即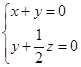 ,令
,令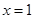 则
则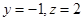 ,
,∴
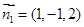 …………………………9分
…………………………9分同理可得平面
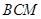 的法向量为
的法向量为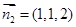 …………………………10分
…………………………10分∴
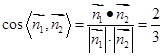 …………………………11分
…………………………11分又易知二面角
 的平面角为钝角,
的平面角为钝角,∴二面角
 的余弦值为
的余弦值为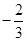 …………………………12分
…………………………12分
练习册系列答案
相关题目
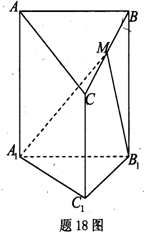
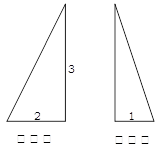
 中,底面
中,底面 是矩形,且
是矩形,且 ,
, ,
, 平面
平面 、
、 分别是线段
分别是线段 、
、 的中点.
的中点.
 ;
; 上是否存在点
上是否存在点 ,使得
,使得 ∥平面
∥平面 ;
; 与平面
与平面 ,求二面角
,求二面角 的余弦值.
的余弦值.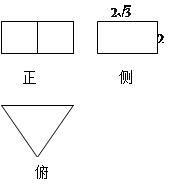




 的斜二侧直观图如图所示,则
的斜二侧直观图如图所示,则