题目内容
3.设an=$\frac{1}{n}$sin$\frac{nπ}{5}$,Sn=a1+a2+…+an,在S1,S2,…,S2014中,正数的个数是( )| A. | 806 | B. | 1007 | C. | 1612 | D. | 2014 |
分析 首先求出函数的周期,结合正弦函数的图象可得前4项为正,第5项为0,由诱导公式可得第6至9项为负,第10项为0,再由f(n)=$\frac{1}{n}$单调递减可得数列的S1,S2,…,S10都为正,同理可得S1,S2,…,S2014均为正.
解答 解:由于an=$\frac{1}{n}$sin$\frac{nπ}{5}$的周期T=10,
由正弦函数性质可知,a1,a2,…,a4>0,a5=0,a6,a7,…,a9<0,a10=0,
且sin$\frac{6π}{5}$=-sin$\frac{π}{5}$,sin$\frac{7π}{5}$=-sin$\frac{2π}{5}$,…,
而f(n)=$\frac{1}{n}$单调递减,
a6…a9都为负数,但是|a6|<a1,|a7|<a2,…,|a9|<a4,
∴S1,S2,…,S5中都为正,而S6,S7,…,S10都为正,
同理S11,S12,…,S20都为正,
S1,S2,…,S2014都为正,
故选:D.
点评 本题考查由数列的通项公式求数列的前n项和,考查三角函数的图象和性质,关键是对于规律的发现,是中档题.

练习册系列答案
相关题目
8.若两个等差数列{an}、{bn}前n项和分别为An,Bn,且满足$\frac{{A}_{n}}{{B}_{n}}$=$\frac{4n+2}{5n-5}$,则$\frac{{a}_{4}+{a}_{14}}{{b}_{8}+{b}_{10}}$的值为( )
| A. | $\frac{7}{9}$ | B. | $\frac{7}{8}$ | C. | $\frac{19}{20}$ | D. | $\frac{8}{7}$ |
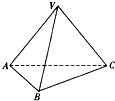 如图,三棱锥V-ABC的底面为正三角形,侧面VAC与底面垂直,且VA=VC,已知其侧(左)视图的面积为$\sqrt{3}$,其正(主)视图的面积为2.
如图,三棱锥V-ABC的底面为正三角形,侧面VAC与底面垂直,且VA=VC,已知其侧(左)视图的面积为$\sqrt{3}$,其正(主)视图的面积为2.