题目内容
17.已知函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x}-1(x≤0)}\\{f(x-1)(x>0)}\end{array}\right.$,则函数g(x)=f(x)-lgx零点个数为10个.分析 分别作出函数,y=($\frac{1}{2}$)x-1的图象,运用平移的方法画出函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x}-1(x≤0)}\\{f(x-1)(x>0)}\end{array}\right.$,利用数形结合求出函数f(x)与m(x)=lgx交点的个数即可得出g(x)=f(x)-lgx零点个数.
解答 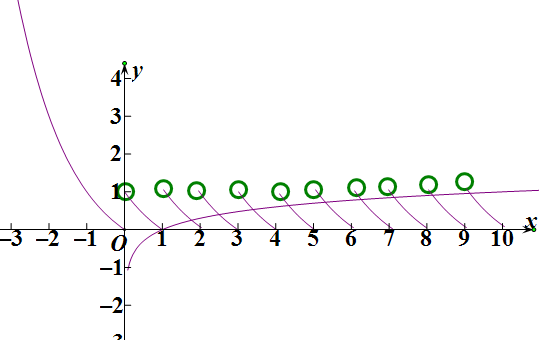 解:∵函数g(x)=f(x)-lgx零点个数,
解:∵函数g(x)=f(x)-lgx零点个数,
∴可以转化为函数f(x)与m(x)=lgx交点的个数,
画出图象得出:lg10=1,f(10)=0,
根据图象可判断函数有10个交点,
故g(x)=f(x)-lgx零点个数为10.
故答案为:10
点评 本题考查函数的图象,函数零点知识,考查函数与方程,数形结合的思想,准确画好图是解决本题的关键

练习册系列答案
相关题目
2.设集合P={-1,0,1},Q={x|$\sqrt{x}$<$\sqrt{2}$},则P∩Q=( )
| A. | {0,1} | B. | {1} | C. | {0} | D. | {-1,0,1} |
3.设an=$\frac{1}{n}$sin$\frac{nπ}{5}$,Sn=a1+a2+…+an,在S1,S2,…,S2014中,正数的个数是( )
| A. | 806 | B. | 1007 | C. | 1612 | D. | 2014 |