题目内容
13.已知函数f(x)=$\sqrt{3}$sinxsin($\frac{π}{2}$+x)+sin(π+x)sinx,x∈R.(1)求函数f(x)的最小正周期和单调递增区间;
(2)设A,B,C是△ABC的三个内角,且f($\frac{A}{2}$)=0,f($\frac{B}{2}$)=$\frac{1}{10}$,求f($\frac{C}{2}$)的值.
分析 (1)利用两角和公式和二倍角公式对函数解析式化简,根据三角函数图象与性质求得函数的最小正周期和单调增区间.
(2)根据题意分别求得sin(A+$\frac{π}{6}$)和sin(B+$\frac{π}{6}$)的值,进而求得cos(A+$\frac{π}{6}$)和cos(B+$\frac{π}{6}$)的值,利用两角和公式求得sin(C+$\frac{π}{6}$),则f($\frac{C}{2}$)的值可得.
解答 解:(1)f(x)=$\sqrt{3}$sinxcosx-sin2x=$\frac{\sqrt{3}}{2}$sin2x+$\frac{cos2x}{2}$-$\frac{1}{2}$=sin(2x+$\frac{π}{6}$)-$\frac{1}{2}$,
∴函数的最小正周期T=$\frac{2π}{2}$=π,
当2kπ$-\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ$+\frac{π}{2}$时,即kπ-$\frac{π}{3}$≤x≤kπ$+\frac{π}{6}$时,k∈Z,函数单调增,
故函数的单调增区间为[kπ-$\frac{π}{3}$,kπ$+\frac{π}{6}$](k∈Z).
(2)f($\frac{A}{2}$)=sin(A+$\frac{π}{6}$)-$\frac{1}{2}$=0,
∴sin(A+$\frac{π}{6}$)=$\frac{1}{2}$,
∵0<A<π,
∴A=$\frac{2π}{3}$,
∴cos(A+$\frac{π}{6}$)=-$\frac{\sqrt{3}}{2}$,
同理f($\frac{B}{2}$)=sin(B+$\frac{π}{6}$)-$\frac{1}{2}$=$\frac{1}{10}$,
∴sin(B+$\frac{π}{6}$)=$\frac{3}{5}$,
∵0<B<$\frac{π}{6}$,
∴cos(B+$\frac{π}{6}$)=$\frac{4}{5}$,
∴cos(A+B+$\frac{π}{3}$)=cos(A+$\frac{π}{6}$)cos(B+$\frac{π}{6}$)-sin(A+$\frac{π}{6}$)sin(B+$\frac{π}{6}$)=-$\frac{\sqrt{3}}{2}$×$\frac{4}{5}$-$\frac{1}{2}$×$\frac{3}{5}$=$\frac{4\sqrt{3}-3}{10}$,
sin(C+$\frac{π}{6}$)=sin(π-A-B+$\frac{π}{2}$$-\frac{π}{3}$)=-cos(A+B+$\frac{π}{3}$)=$\frac{3-4\sqrt{3}}{10}$,
∴f($\frac{C}{2}$)=sin(C+$\frac{π}{6}$)-$\frac{1}{2}$=$\frac{3-4\sqrt{3}-5}{10}$=-$\frac{2\sqrt{3}+1}{5}$.
点评 本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.解题过程中注意公式的熟练运用.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案| A. | 806 | B. | 1007 | C. | 1612 | D. | 2014 |
| A. | [0,$\frac{8}{9}$] | B. | [$\frac{1}{9}$,$\frac{5}{9}$] | C. | [$\frac{2}{3}$,$\frac{8}{9}$] | D. | [0,$\frac{4}{9}$] |
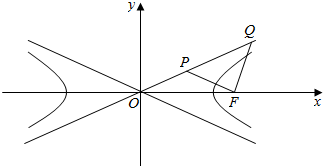
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
 如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的C处恰有一可旋转光源满足甲水果生产的需要,该光源照射范围是∠ECF=$\frac{π}{6}$,点E,F的直径AB上,且∠ABC=$\frac{π}{6}$.
如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的C处恰有一可旋转光源满足甲水果生产的需要,该光源照射范围是∠ECF=$\frac{π}{6}$,点E,F的直径AB上,且∠ABC=$\frac{π}{6}$.