题目内容
15.证明:(a+b)(a2+b2)(a3+b3)≥8a3b3.分析 直接化简不等式的左侧,然后利用综合法,集合均值不等式证明即可.
解答 证明:左侧(a+b)(a2+b2)(a3+b3)=(a+b)2(a2+b2)(a2+b2-ab).
∵a2+b2≥2ab,(a+b)2≥4ab,a2+b2-ab≥ab,当且仅当a=b时取等号,
∴(a+b)2(a2+b2)(a2+b2-ab)≥8a3b3.
即(a+b)(a2+b2)(a3+b3)≥8a3b3.
点评 本题考查不等式的证明,综合法的应用,考查逻辑推理能力.不可直接三个因式利用综合法,否则需要讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.设an=$\frac{1}{n}$sin$\frac{nπ}{5}$,Sn=a1+a2+…+an,在S1,S2,…,S2014中,正数的个数是( )
| A. | 806 | B. | 1007 | C. | 1612 | D. | 2014 |
5.如图,已知F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,P、Q在渐近线上,PQ的中垂线过点F,O是坐标原点,若∠PFQ=Rt∠,OQ=3OP,则双曲线的离心率等于( )
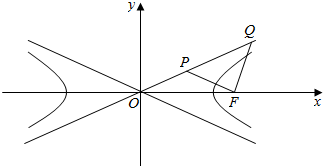

| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |