题目内容
设 为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时, =0,当四点不共面时,
=0,当四点不共面时, 的值为四点组成的四面体的体积.
的值为四点组成的四面体的体积.
(1)求概率P( =0);
=0);
(2)求 的分布列,并求其数学期望E (
的分布列,并求其数学期望E ( ).
).
 为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时, =0,当四点不共面时,
=0,当四点不共面时, 的值为四点组成的四面体的体积.
的值为四点组成的四面体的体积.(1)求概率P(
 =0);
=0);(2)求
 的分布列,并求其数学期望E (
的分布列,并求其数学期望E ( ).
).(1)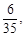
(2)
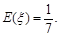
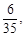
(2)
 | 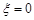 | 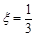 | 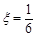 |
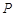 | 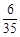 | 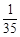 | 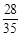 |
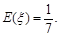
试题分析:(1)求概率P(
 = 0),就是求四点共面时概率.古典概型概率
= 0),就是求四点共面时概率.古典概型概率 的求法,关键要找出
的求法,关键要找出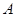 所包含的基本事件个数,然后套用公式
所包含的基本事件个数,然后套用公式
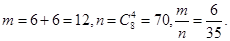 (2)求
(2)求 的数学期望的基本步骤:首先理解
的数学期望的基本步骤:首先理解 的意义,写出
的意义,写出 可能取的全部值,本题考虑四个顶点不同位置,求体积;其次求
可能取的全部值,本题考虑四个顶点不同位置,求体积;其次求 取各个值的概率,写出概率分布;最后根据概率分布,由数学期望的定义求出
取各个值的概率,写出概率分布;最后根据概率分布,由数学期望的定义求出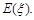
试题解析:(1)从正方体的八个顶点中任取四个点,共有
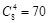 种不同取法.
种不同取法.其中共面的情况共有12种(6个侧面,6个对角面).
则
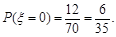 3分
3分(2)任取四个点,当四点不共面时,四面体的体积只有以下两种情况:
①四点在相对面且异面的对角线上,体积为
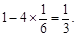
这样的取法共有2种. 5分
②四点中有三个点在一个侧面上,另一个点在相对侧面上,体积为
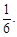
这样的取法共有
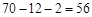 种 7分
种 7分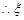 的分布列为
的分布列为 | 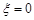 | 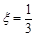 | 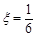 |
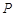 | 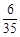 | 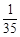 | 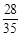 |
数学期望
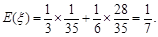 10分
10分
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 ,甲、丙两人同时不能被聘用的概率是
,甲、丙两人同时不能被聘用的概率是 ,乙、丙两人同时能被聘用的概率为
,乙、丙两人同时能被聘用的概率为 ,且三人各自能否被聘用相互独立.
,且三人各自能否被聘用相互独立. 为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求
为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求 表示至第2分钟末已买完饭的人数,求
表示至第2分钟末已买完饭的人数,求 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 (i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
(i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大? .
. 的分布列和数学期望.
的分布列和数学期望. 