题目内容
一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
从第一个学生开始买饭时计时.
(Ⅰ)估计第三个学生恰好等待4分钟开始买饭的概率;
(Ⅱ) 表示至第2分钟末已买完饭的人数,求
表示至第2分钟末已买完饭的人数,求 的分布列及数学期望
的分布列及数学期望
| 买饭时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
(Ⅰ)估计第三个学生恰好等待4分钟开始买饭的概率;
(Ⅱ)
 表示至第2分钟末已买完饭的人数,求
表示至第2分钟末已买完饭的人数,求 的分布列及数学期望
的分布列及数学期望(Ⅰ)第2分钟末没有人买晚饭的概率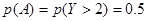 ;(Ⅱ)第三个学生恰好等待4分钟开始买饭的概率
;(Ⅱ)第三个学生恰好等待4分钟开始买饭的概率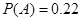 .
.
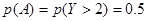 ;(Ⅱ)第三个学生恰好等待4分钟开始买饭的概率
;(Ⅱ)第三个学生恰好等待4分钟开始买饭的概率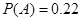 .
.试题分析:(Ⅰ)估计第三个学生恰好等待4分钟开始买饭的概率,包括①第一个学生买饭所需的时间为1分钟,且第二个学生买饭所需的时间为3分钟;②第一个学生买饭所需的时间为3分钟,且第二个学生买饭所需的时间为1分钟;③第一个和第二个学生买饭所需的时间均为2分钟.这三个事件,根据互斥事件的概率求法,即可求出概率;(Ⅱ)
 表示至第2分钟末已买完饭的人数,包括三种情况, 第2分钟末没有人买晚饭,第2分钟末有一人买饭,它包括:第一个学生买饭所需的时间为1分钟且第二个学生买饭所需的时间超过1分钟,或第一个学生买饭所需的时间为2分钟,第2分钟末,有两人买饭,故
表示至第2分钟末已买完饭的人数,包括三种情况, 第2分钟末没有人买晚饭,第2分钟末有一人买饭,它包括:第一个学生买饭所需的时间为1分钟且第二个学生买饭所需的时间超过1分钟,或第一个学生买饭所需的时间为2分钟,第2分钟末,有两人买饭,故 所有可能的取值为
所有可能的取值为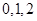 ,分别求出概率,从而写出
,分别求出概率,从而写出 的分布列,求出数学期望.
的分布列,求出数学期望.试题解析:(Ⅰ)设
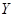 表示学生买饭所需的时间,用频率估计概率,得
表示学生买饭所需的时间,用频率估计概率,得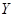 的分布列如下:
的分布列如下: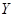 | 1 | 2 | 3 | 4 | 5 |
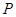 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
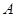 表示事件“第三个学生恰好等待4分钟开始买饭”,则事件A对应三种情形:
表示事件“第三个学生恰好等待4分钟开始买饭”,则事件A对应三种情形: ①第一个学生买饭所需的时间为1分钟,且第二个学生买饭所需的时间为3分钟;②第一个学生买饭所需的时间为3分钟,且第二个学生买饭所需的时间为1分钟;③第一个和第二个学生买饭所需的时间均为2分钟.
所以
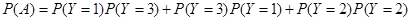
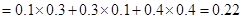 (6分)
(6分)(Ⅱ)
 所有可能的取值为
所有可能的取值为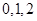
 对应第一个学生买饭所需的时间超过2分钟,
对应第一个学生买饭所需的时间超过2分钟,所以
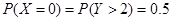
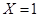 对应第一个学生买饭所需的时间为1分钟且第二个学生买饭所需的时间超过1分钟,或第一个学生买饭所需的时间为2分钟.
对应第一个学生买饭所需的时间为1分钟且第二个学生买饭所需的时间超过1分钟,或第一个学生买饭所需的时间为2分钟. 所以
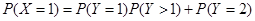
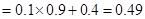
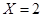 对应两个学生买饭所需时间均为1分钟,
对应两个学生买饭所需时间均为1分钟, 所以
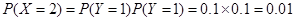
所以
 的分布列为
的分布列为 | 0 | 1 | 2 |
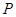 | 0.5 | 0.49 | 0.01 |
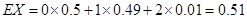 (12分)
(12分)
练习册系列答案
相关题目

 (
( ≥0)万元,投资B项目资金为
≥0)万元,投资B项目资金为 (
( ≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利
≥0)万元,调研结果是:未来一年内,位于一类风区的A项目获利 的可能性为
的可能性为 ,亏损
,亏损 的可能性为
的可能性为 ;位于二类风区的B项目获利
;位于二类风区的B项目获利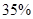 的可能性为
的可能性为 的可能性是
的可能性是 ,不赔不赚的可能性是
,不赔不赚的可能性是 .
. 和
和 ,试写出随机变量
,试写出随机变量 ,
, ;
; 万元的资金投资于A,B项目,且公司要求对A项目的投
万元的资金投资于A,B项目,且公司要求对A项目的投 的最大值.
的最大值. 为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时, 个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖. ,求抽奖者获奖的概率;
,求抽奖者获奖的概率; 表示获奖的人数,求
表示获奖的人数,求 .
.
 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求 ,则方差V(X)的值是________.
,则方差V(X)的值是________.
 的所有非空子集中,等可能地取出一个.
的所有非空子集中,等可能地取出一个.  :集合中的所有元素之和为10,求所取出的非空子集满足性质
:集合中的所有元素之和为10,求所取出的非空子集满足性质 ,求
,求 .
.