题目内容
袋子里有完全相同的3只红球和4只黑球,今从袋子里随机取球.
(Ⅰ)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;
(Ⅱ)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;
(Ⅱ)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分
 的分布列和数学期望.
的分布列和数学期望. (1)108:343
(2)

(2)
 | 3 | 4 | 5 | 6 |
 |  |  |  |  |

试题分析:解:(Ⅰ)从袋子里有放回地取3次球,相当于做了3次独立重复试验,每次试验取出红球的概率为
 ,取出黑球的概率为
,取出黑球的概率为 ,设事件
,设事件 “取出2个红球1个黑球”,则
“取出2个红球1个黑球”,则 6分
6分(Ⅱ)
 的取值有四个:3、4、5、6,分布列为:
的取值有四个:3、4、5、6,分布列为: ,
, ,
, ,
, .
. | 3 | 4 | 5 | 6 |
 |  |  |  |  |
10分
从而得分
 的数学期望
的数学期望 .0 12分
.0 12分点评:主要是考查了分布列的求解以及期望值的运用,属于基础题。

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目

 名学生被考官L面试,求
名学生被考官L面试,求 为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
 表示抽到“极幸福”的人数,求
表示抽到“极幸福”的人数,求


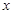 个红球与
个红球与 个白球(
个白球( ,且
,且 ),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。
),乙箱中放有2个红球、1个白球与1个黑球。从甲箱中任取2个球,从乙箱中任取1个球。 ,求当
,求当 时,求取出的3个球中红球个数
时,求取出的3个球中红球个数 的期望
的期望 。
。
 ,
,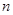 ,平均数为
,平均数为 ,则
,则 ( )
( ) 。
。 层楼,写出
层楼,写出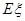 。
。