题目内容
某电器商经过多年的经验发现本店每个月售出的电冰箱的台数ξ是一个随机变量,它的分布列为P(ξ=i)= (i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
(i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
 (i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
(i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?电器商每月初购进9或10台电冰箱时,月收益最大,最大收益为1500元.
设x为电器商每月初购进的冰箱的台数,依题意,只需考虑1≤x≤12的情况.设电器商每月的收益为y元,则y是随机变量ξ的函数,且y=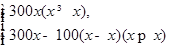 于是电器商每月获益的平均数,即为数学期望Ey=300x(Px+Px+1+…+P12)+[300-100(x-1)]P1+[2×300-100(x-2)]P2+…+[(x-1)×300-100]Px-1=300x(12-x+1)·
于是电器商每月获益的平均数,即为数学期望Ey=300x(Px+Px+1+…+P12)+[300-100(x-1)]P1+[2×300-100(x-2)]P2+…+[(x-1)×300-100]Px-1=300x(12-x+1)· +
+
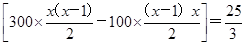 (-2x2+38x).
(-2x2+38x).
因为x∈N*,所以当x=9或x=10时,数学期望最大.
故电器商每月初购进9或10台电冰箱时,月收益最大,最大收益为1500元.
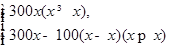 于是电器商每月获益的平均数,即为数学期望Ey=300x(Px+Px+1+…+P12)+[300-100(x-1)]P1+[2×300-100(x-2)]P2+…+[(x-1)×300-100]Px-1=300x(12-x+1)·
于是电器商每月获益的平均数,即为数学期望Ey=300x(Px+Px+1+…+P12)+[300-100(x-1)]P1+[2×300-100(x-2)]P2+…+[(x-1)×300-100]Px-1=300x(12-x+1)· +
+
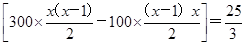 (-2x2+38x).
(-2x2+38x).因为x∈N*,所以当x=9或x=10时,数学期望最大.
故电器商每月初购进9或10台电冰箱时,月收益最大,最大收益为1500元.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目

 名学生被考官L面试,求
名学生被考官L面试,求 为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
 ,求
,求 .
.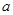 个红球,
个红球,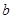 个黄球,
个黄球,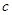 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,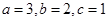 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求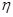 为取出此球所得分数.若
为取出此球所得分数.若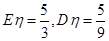 ,求
,求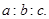
 ,则方差V(X)的值是________.
,则方差V(X)的值是________.