Question

【题目】已知关于x不等式x2﹣2mx+m+2<0（m∈R）的解集为M．

（1）当M为空集时，求m的取值范围；

（2）在（1）的条件下，求的最大值；

（3）当M不为空集，且M [1，4]时，求实数m的取值范围．

Answer 1

【答案】(1) 实数m的取值范围为（﹣1，2）;(2) 的最小值为 ;(3) a的取值范围为.

【解析】试题分析：

（1） 为空集时 ，由此求出 的取值范围；
(2) 由（1）知 ，则 函数化为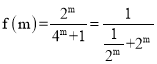 ,利用基本不等式可求出其最大值

（3）设，讨论M为空集和M不为空集时，利用判别式，结合图象求出实数m的取值范围．

试题解析：（1）∵M为空集，

∴△=4m2﹣4（m+2）＜0，即m2﹣m﹣2＜0

∴实数m的取值范围为（﹣1，2）.

（2）由（1）知m∈（﹣1，2），则m+1>0，

∴f(m)=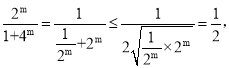

即f(m)= 当且仅当，即时取等号.

所以

（3）令f（x）=x2﹣2ax+a+2=（x﹣a）2﹣a2+a+2，

当M不为空集时，由M[1，4]，得

．综上，实数a的取值范围为