题目内容
某大厦的一部电梯从底层出发后只能在第18,19,20层可以停靠，若该电梯在底层载有5位乘客，且每位乘客在这三层的每一层下电梯的概率均为
，用X表示这5位乘客在第20层下电梯的人数，求随机变量X的分布列．
X的分布列为X 0 1 2 3 4 5 P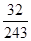 
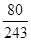
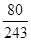
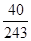
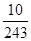
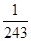
解析解：考查每一位乘客是否在第20层下电梯为一次试验，这是5次独立重复试验，即X～B
，
即有P(X＝k)＝C5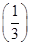k
k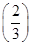
5－k，k＝0,1,2,3,4,5，
从而X的分布列为X 0 1 2 3 4 5 P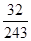
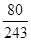
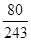
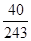
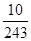
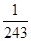
练习册系列答案
相关题目
为了解甲、乙两个快递公司的工作状况，假设同一个公司快递员的工作状况基本相同，现从甲、乙两公司各随机抽取一名快递员，并从两人某月（30天）的快递件数记录结果中随机抽取10天的数据，制表如下：
| 甲公司某员工A | | 乙公司某员工B | ||||||||||||
| 3 | 9 | 6 | 5 | 8 | 3 | 3 | 2 | 3 | 4 | 6 | 6 | 6 | 7 | 7 |
| | | | | | | 0 | 1 | 4 | 4 | 2 | 2 | 2 | | |
甲公司规定每件4.5元；乙公司规定每天35件以内（含35件）的部分每件4元，超出35件的部分每件7元.
（1）根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数；
（2）为了解乙公司员工B的每天所得劳务费的情况，从这10天中随机抽取1天，他所得的劳务费记为
（单位：元），求的分布列和数学期望；（3）根据表中数据估算两公司的每位员工在该月所得的劳务费.
