题目内容
已知一个矩形由三个相同的小矩形拼凑而成(如图所示),用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,求:
(1)3个矩形都涂同一颜色的概率;
(2)3个小矩形颜色都不同的概率.
(1)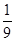 ;(2)
;(2)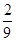 .
.
解析试题分析:(1)利用分步乘法原理即可得出涂完三个矩形共有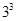 种方法,而3个矩形都涂同一颜色的方法只有三种,利用古典概型的概率计算公式即可得出;(2)“3个小矩形颜色都不同”相当于把三种颜色的全排列数,即
种方法,而3个矩形都涂同一颜色的方法只有三种,利用古典概型的概率计算公式即可得出;(2)“3个小矩形颜色都不同”相当于把三种颜色的全排列数,即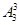 种涂法.利用古典概型的概率计算公式即可得出.
种涂法.利用古典概型的概率计算公式即可得出.
试题解析:(1)由题意可知:用三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,可以分三步去完成:
涂第一个矩形可有三种方法,涂第二个矩形可有三种方法,涂第三个矩形可有三种方法,
由分步乘法原理可得涂完三个矩形共有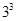 =27种方法,其中3个矩形都涂同一颜色的方法只有三种.
=27种方法,其中3个矩形都涂同一颜色的方法只有三种.
设“3个矩形都涂同一颜色”为事件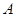 ,则
,则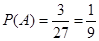 .
.
(2)由(1)可知:三种不同颜色给3个小矩形涂色,每个小矩形只涂一种颜色,方法共有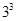 .
.
设“3个小矩形颜色都不同”为事件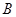 ,则事件
,则事件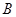 包括
包括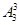 种涂法.
种涂法.
由古典概型的概率计算公式可得: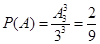 .
.
考点:1、古典概型的概率;2、排列的应用.

练习册系列答案
相关题目
年龄在60岁(含60岁)以上的人称为老龄人,某地区老龄人共有35万,随机调查了该地区700名老龄人的健康状况,结果如下表:
| 健康指数 | 2 | 1 | 0 | -1 |
| 60岁至79岁的人数 | 250 | 260 | 65 | 25 |
| 80岁及以上的人数 | 20 | 45 | 20 | 15 |
(1)估计该地区80岁以下老龄人生活能够自理的概率。
(2)若一个地区老龄人健康指数的平均值不小于1.2,则该地区可被评为“老龄健康地区”.
请写出该地区老龄人健康指数X分布列,并判断该地区能否被评为“老龄健康地区”.
某单位从一所学校招收某类特殊人才.对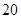 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
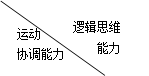 | 一般 | 良好 | 优秀 |
| 一般 |  |  |  |
| 良好 | 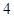 |  |  |
| 优秀 |  |  | 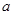 |
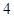 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这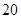 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为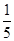 .
.(1)求
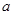 ,
, 的值;
的值;(2)从运动协调能力为优秀的学生中任意抽取
 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率. 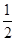 ,且各件产品是否为优质品相互独立.
,且各件产品是否为优质品相互独立.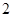 月
月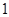 日至
日至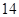 日的空气质量指数趋势图,空气质量指数(
日的空气质量指数趋势图,空气质量指数(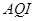 )小于
)小于 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于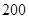 表示空气重度污染,某人随机选择
表示空气重度污染,某人随机选择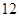 日中的某一天到达该市,并停留
日中的某一天到达该市,并停留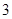 天.
天.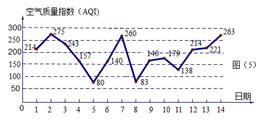
 .
. ,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
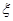 ,求
,求