题目内容
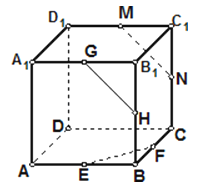
【题目】如图是一个正方体的展开图,如果将它还原为正方体,那么NC、DE、AF、BM这四条线段所在的直线是异面直线的有多少对?试以其中一对为例进行证明.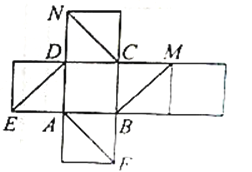
【答案】解:如图所示: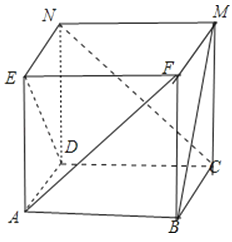 ,
,
把展开图再还原成正方体,由经过平面外一点和平面内一点的直线和平面内
不经过该点的直线是异面直线可得,NC、DE、AF、BM这四条线段所在直线是异面直线的有:
AF和BM,AF和NC,AF和DE,BM和NC,BM和DE,NC和DE,共6对,
比如:BM和AF是异面直线,
证明如下:
∵F点在平面BCM中,A点在平面BCM外,
直线BM不经过F点,
由异面直线的定义,得到AF和BM是异面直线
【解析】先把正方体的展开图再还原成正方体,利用异面直线的判定定理找出NC、DE、AF、BM中的异面直线.
【考点精析】解答此题的关键在于理解异面直线的判定的相关知识,掌握过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线).

练习册系列答案
相关题目
【题目】某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如下图).记成绩不低于90分者为“成绩优秀”.
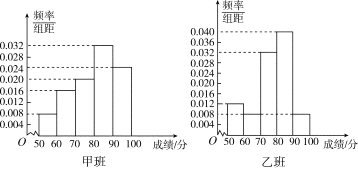
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
附:![]() .
.
P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |