题目内容
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() (
(![]() ).
).
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,
, ![]() ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和,求正整数
项和,求正整数![]() ,使得对任意
,使得对任意![]() 均有
均有![]() 恒成立;
恒成立;
(3)设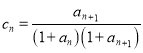 ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和,若对任意
项和,若对任意![]() 均有
均有![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]() 或5(3)
或5(3)![]()
【解析】试题分析: (1)由![]() 与
与![]() 之间的关系求出
之间的关系求出![]() 的通项公式; (2)先求出数列
的通项公式; (2)先求出数列![]() 的通项公式,方法一是求出
的通项公式,方法一是求出![]() 增减情况,正负情况,求出
增减情况,正负情况,求出![]() 的最大项,方法二是求出
的最大项,方法二是求出![]() 的前n项和
的前n项和![]() ,再求出
,再求出![]() ,得出
,得出![]() 的增减性,再求出
的增减性,再求出![]() 的最大值; (3)用裂项相消法求出数列
的最大值; (3)用裂项相消法求出数列![]() 的前n项和
的前n项和![]() ,
, ![]() ,再求出
,再求出![]() 的范围.
的范围.
试题解析: 由![]() ,得
,得![]() 两式相减,得
两式相减,得![]()
∴![]()
数列![]() 为等比数列,公比
为等比数列,公比![]()
又![]() ,得
,得![]() ,
, ![]() ∴
∴ ![]()
(2)![]()
![]()
![]() ,
, ![]()
方法一当![]() 时,
时, ![]()
![]()
因此, ![]()
![]()
∴ 对任意![]() 均有
均有![]() ,故
,故![]() 或
或![]() 。
。
方法二(![]()
![]()
两式相减,得![]()
![]() =
=![]() ,
,
![]() ,
,
当![]() ,当
,当![]() ,当
,当![]() 时,
时, ![]() ,
,
综上,当且仅当![]() 或5时,均有
或5时,均有![]()
(3)∵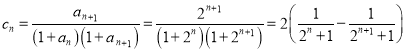
∴ ![]()
![]()
∵对任意![]() 均有
均有![]() 成立,
成立,
∴![]() ,
,
所以![]() 的最小值为
的最小值为![]()
点睛: 本题主要考查了数列有关问题,涉及的知识点有求数列通项公式,用裂项相消法求和,判断数列的增减性等,属于中档题.

练习册系列答案
相关题目