题目内容
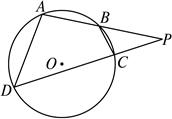
如图,已知PE切⊙O于点E,割线PBA交⊙O于A,B两点,∠APE的平分线和AE,BE分别交于点C,D.
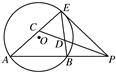
求证:(1)CE=DE;(2)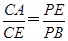 .
.

求证:(1)CE=DE;(2)
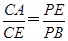 .
.(1)见解析(2)见解析
(1)∵PE切⊙O于点E,∴∠A=∠BEP.
∵PC平分∠APE,∴∠A+∠CPA=∠BEP+∠DPE.
又∠ECD=∠A+∠CPA,∠EDC=∠BEP+∠DPE,
∴∠ECD=∠EDC,∴EC=ED.
(2)∵∠PDB=∠EDC,∠EDC=∠ECD,∴∠PDB=∠PCE.
又∠BPD=∠EPC,∴△PBD∽△PEC,∴ .
.
同理△PDE∽△PCA,∴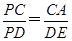 .∴
.∴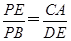 .
.
又DE=CE,∴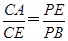 .
.
∵PC平分∠APE,∴∠A+∠CPA=∠BEP+∠DPE.
又∠ECD=∠A+∠CPA,∠EDC=∠BEP+∠DPE,
∴∠ECD=∠EDC,∴EC=ED.
(2)∵∠PDB=∠EDC,∠EDC=∠ECD,∴∠PDB=∠PCE.
又∠BPD=∠EPC,∴△PBD∽△PEC,∴
 .
.同理△PDE∽△PCA,∴
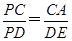 .∴
.∴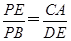 .
.又DE=CE,∴
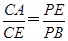 .
.
练习册系列答案
相关题目
 是⊙
是⊙ 的直径,
的直径,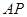 是⊙
是⊙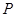 ,
,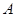 为切点.若
为切点.若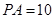 ,
,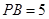 ,
,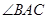 的平分线
的平分线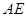 与
与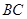 和⊙
和⊙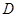 、
、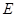 ,求
,求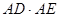 的值.
的值.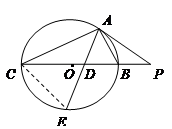
 ,求圆O的半径长和∠EFD的大小.
,求圆O的半径长和∠EFD的大小.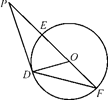
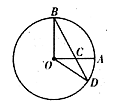

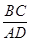 的值为________.
的值为________.