题目内容
已知数列{an}的前n项和 ,
,
(1)求通项公式an ;(2)令 ,求数列{bn}前n项的和Tn.
,求数列{bn}前n项的和Tn.
 ,
,(1)求通项公式an ;(2)令
 ,求数列{bn}前n项的和Tn.
,求数列{bn}前n项的和Tn.(1)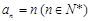 (2)
(2)
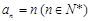 (2)
(2)
试题分析:解:(1)当n≥2时,
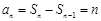 3分
3分又
 ,也满足上式,所以
,也满足上式,所以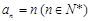 4分
4分(2)
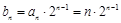 ,所以
,所以 ,
, , 两式相减,得
, 两式相减,得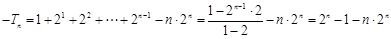
所以,
 8分
8分点评:主要是考查了等比数列的错位相减法求和的运用也是高考的热点,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前n项和
的前n项和 ,则( )
,则( ) 的前
的前 项和
项和 满足
满足 ,等差数列
,等差数列 满足
满足 ,
, .
. ,数列
,数列 的前
的前 ,求证
,求证 .
. 满足:
满足: ,数列
,数列 满足
满足 .
. 求
求 的值及
的值及 的等比数列,问是否存在正实数
的等比数列,问是否存在正实数 ,使得数列
,使得数列 的前
的前 项和
项和 (用n,
(用n, 表示).
表示).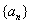 中,
中,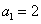 ,
,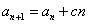 (
(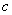 是常数,
是常数,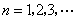 ),且
),且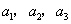 成公比不为
成公比不为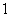 的等比数列,则
的等比数列,则 共有
共有 项,其中奇数项通项公式为
项,其中奇数项通项公式为 ,则数列
,则数列



 中,
中, ,则
,则 中,
中, ,
,  ,则
,则 ( )
( ) 



 的前
的前 项和为
项和为 ,若对任意
,若对任意 ,都有
,都有 .
. 是等比数列,并求数列
是等比数列,并求数列 满足
满足 ,问是否存在
,问是否存在 ,使得
,使得 恒成立?如果存在,求出
恒成立?如果存在,求出