题目内容
数列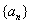 中,
中,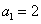 ,
,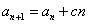 (
(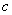 是常数,
是常数,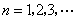 ),且
),且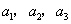 成公比不为
成公比不为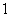 的等比数列,则
的等比数列,则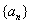 的通项公式是 .
的通项公式是 .
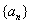 中,
中,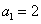 ,
,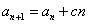 (
(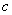 是常数,
是常数,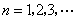 ),且
),且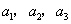 成公比不为
成公比不为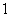 的等比数列,则
的等比数列,则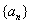 的通项公式是 .
的通项公式是 .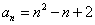
试题分析:a1=2,a2=2+c,a3=2+3c,因为a1,a2,a3成等比数列,所以(2+c)2=2(2+3c),解得c=0或c=2.当c=0时,a1=a2=a3,不符合题意舍去,故c=2.当n≥2时,由于a2-a1=c,a3-a2=2c,an-an-1=(n-1)c,所以an-a1=[1+2++(n-1)]c=
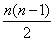 c.又a1=2,c=2,故an=2+n(n-1)=n2-n+2(n=2,3,).当n=1时,上式也成立,所以an=n2-n+2
c.又a1=2,c=2,故an=2+n(n-1)=n2-n+2(n=2,3,).当n=1时,上式也成立,所以an=n2-n+2点评:掌握常见数列通项公式的求法如叠加法、叠乘法是解决此类问题的关键,解题时要注意计算能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
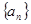 满足:
满足: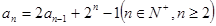 且
且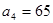 .(1)求数列
.(1)求数列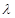 ,使数列
,使数列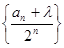 为等差数列?若存在,求出
为等差数列?若存在,求出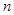 项和
项和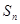 .
. 的通项公式
的通项公式 ,其前
,其前 项和为
项和为 ,则
,则 等于 ( )
等于 ( )



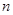 项正项数列为
项正项数列为 ,其前
,其前 ,定义
,定义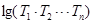 为“相对叠乘积”,如果有2013项的正项数列
为“相对叠乘积”,如果有2013项的正项数列 的“相对叠乘积”为
的“相对叠乘积”为 ,则有2014项的数列
,则有2014项的数列 的“相对叠乘积”为_______。
的“相对叠乘积”为_______。 ,且
,且 ,则
,则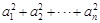 =___________
=___________ ,
, ,求数列{bn}前n项的和Tn.
,求数列{bn}前n项的和Tn.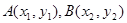 是函数
是函数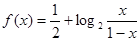 图象上任意两点,且
图象上任意两点,且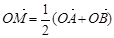 ,已知点
,已知点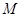 的横坐标为
的横坐标为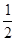 ,且有
,且有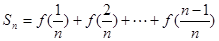 ,其中
,其中 且n≥2,
且n≥2,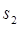 ,
,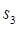 ,
,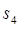 及
及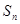 ;
;  ,其中
,其中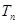 为数列
为数列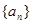 的前n项和,若
的前n项和,若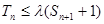 对一切
对一切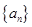 的前n项和记为
的前n项和记为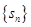 ,已知
,已知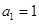 ,
,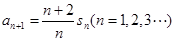 .
.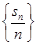 是等比数列;
是等比数列;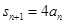 .
.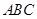 中,角
中,角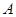 、
、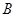 、
、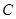 成等差数列,且
成等差数列,且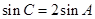 .
.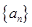 满足
满足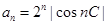 ,前
,前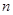 项为和
项为和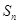 ,若
,若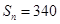 ,求
,求