题目内容
.(本小题满分12分)
已知椭圆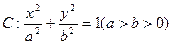 的离心率为
的离心率为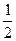 ,且经过点
,且经过点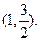
(1)求椭圆C的方程;
(2)已知A为椭圆C的左顶点,直线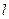 过右焦点F与椭圆C交于M,N两点,若AM、AN的斜率
过右焦点F与椭圆C交于M,N两点,若AM、AN的斜率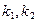 满足
满足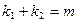 (定值
(定值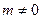 ),求直线
),求直线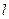 的斜率。
的斜率。
已知椭圆
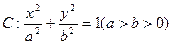 的离心率为
的离心率为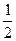 ,且经过点
,且经过点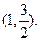
(1)求椭圆C的方程;
(2)已知A为椭圆C的左顶点,直线
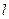 过右焦点F与椭圆C交于M,N两点,若AM、AN的斜率
过右焦点F与椭圆C交于M,N两点,若AM、AN的斜率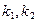 满足
满足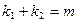 (定值
(定值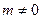 ),求直线
),求直线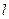 的斜率。
的斜率。解:(1)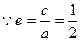
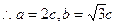 2分
2分
又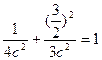
解得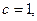
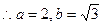 3分
3分
椭圆C的方程是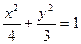 …………………………4分
…………………………4分
(2)若直线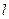 斜率不存在,显然
斜率不存在,显然 不合题意 ………………………………5分
不合题意 ………………………………5分
设直线方程为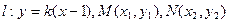
取立方程组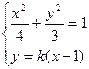 得
得
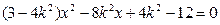 ……………………………………7分
……………………………………7分
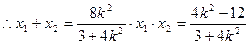 ……………………………………8分
……………………………………8分
又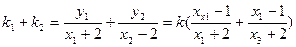
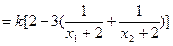
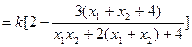
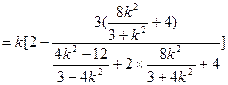
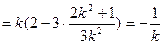 ……………………………………11分
……………………………………11分
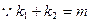
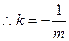 ………………………………………12分
………………………………………12分
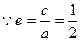
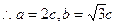 2分
2分又
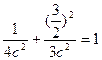
解得
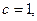
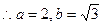 3分
3分椭圆C的方程是
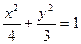 …………………………4分
…………………………4分(2)若直线
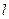 斜率不存在,显然
斜率不存在,显然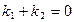 不合题意 ………………………………5分
不合题意 ………………………………5分设直线方程为
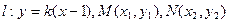
取立方程组
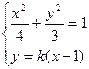 得
得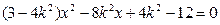 ……………………………………7分
……………………………………7分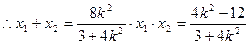 ……………………………………8分
……………………………………8分又
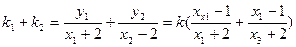
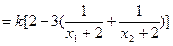
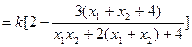
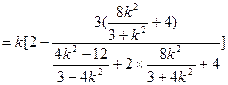
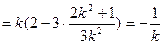 ……………………………………11分
……………………………………11分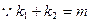
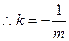 ………………………………………12分
………………………………………12分略

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,长轴长为
轴上,长轴长为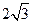 ,离心率为
,离心率为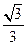 ,经过其左焦点
,经过其左焦点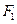 的直线
的直线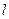 交椭圆
交椭圆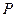 、
、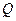 两点(I)求椭圆
两点(I)求椭圆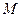 ,使得
,使得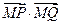 恒为常数?若存在,求出
恒为常数?若存在,求出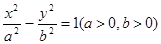 的左、右焦点分别为
的左、右焦点分别为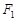 、
、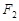 ,点
,点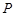 在双曲线的右支上,直线
在双曲线的右支上,直线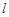 为过
为过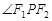 ,过
,过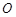 作与直线
作与直线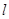 平行的直线交
平行的直线交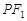 于
于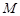 点,则
点,则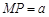 ,利用类比推理:若椭圆
,利用类比推理:若椭圆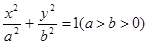 的左、右焦点分别为
的左、右焦点分别为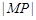 的值为 ( )
的值为 ( ) 
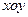 中,设点
中,设点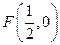 ,直线
,直线 :
: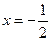 ,点
,点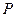 在直线
在直线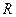 是线段
是线段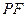 与
与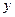 轴的交点,
轴的交点, 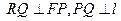 .
.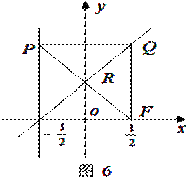
 的轨迹的方程
的轨迹的方程 ;
;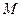 过
过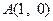 ,且圆心
,且圆心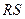 是圆
是圆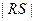 是否为定值?请说明理由.
是否为定值?请说明理由.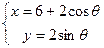 上的动点,(1)若
上的动点,(1)若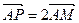 ,试求动点P的
,试求动点P的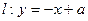 与曲线C相交于不同的两点E、F, O为坐标原点且
与曲线C相交于不同的两点E、F, O为坐标原点且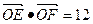 ,求∠EOF的余弦值和实数
,求∠EOF的余弦值和实数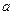 的值.
的值.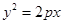 的焦点与双曲线
的焦点与双曲线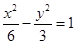 的右焦点重合,则
的右焦点重合,则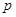 的值为( )
的值为( )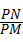 的最小值.
的最小值.
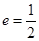 ,求
,求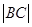 与
与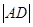 的比值;
的比值;