题目内容
如图边长为2的正方形花园的一角是以A为中心,1为半径的扇形水池.现需在其余部分设计一个矩形草坪PNCQ,其中P是水池边上任意一点,点N、Q分别在边BC和CD上,设∠PAB为θ.
(I)用θ表示矩形草坪PNCQ的面积,并求其最小值;
(II)求点P到边BC和AB距离之比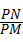 的最小值.
的最小值.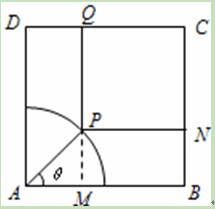
(I)用θ表示矩形草坪PNCQ的面积,并求其最小值;
(II)求点P到边BC和AB距离之比
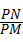 的最小值.
的最小值.
解:(I)因为∠PAB为θ,|AP|=1.
∴AM=COSθ,PM=sinθ,
PN=2﹣cosθ,PQ=2﹣sinθ,
∴矩形草坪PNCQ面积S=(2﹣cosθ)(2﹣sinθ)
=4﹣2(sinθ+cosθ)+sinθ•cosθ
=4﹣2(sinθ+cosθ)+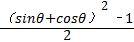
=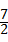 ﹣2
﹣2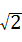 sin(
sin( )+
)+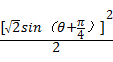
=sin2( )﹣2
)﹣2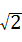 sin(
sin( )+
)+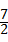
=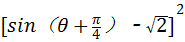 ﹣2+
﹣2+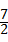 .
.
∵θ∈[0, ],∴
],∴ ∈[
∈[ ].sin(
].sin( )∈[
)∈[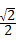 ,1].
,1].
∴当sin( )=1,即θ=
)=1,即θ=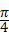 时,面积有最小值此时s=
时,面积有最小值此时s=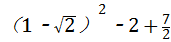 =
= .
.
故当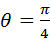 ,最小值为
,最小值为 ;(6分)
;(6分)
(II)∵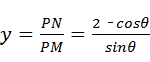
∴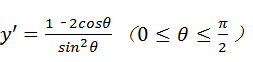 ,令1﹣2cosθ=0⇒
,令1﹣2cosθ=0⇒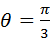 .
.
所以当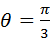 时,
时,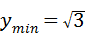 (12分)
(12分)
∴AM=COSθ,PM=sinθ,
PN=2﹣cosθ,PQ=2﹣sinθ,
∴矩形草坪PNCQ面积S=(2﹣cosθ)(2﹣sinθ)
=4﹣2(sinθ+cosθ)+sinθ•cosθ
=4﹣2(sinθ+cosθ)+
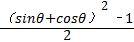
=
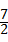 ﹣2
﹣2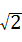 sin(
sin( )+
)+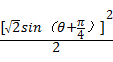
=sin2(
 )﹣2
)﹣2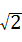 sin(
sin( )+
)+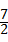
=
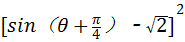 ﹣2+
﹣2+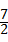 .
.∵θ∈[0,
 ],∴
],∴ ∈[
∈[ ].sin(
].sin( )∈[
)∈[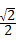 ,1].
,1].∴当sin(
 )=1,即θ=
)=1,即θ=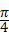 时,面积有最小值此时s=
时,面积有最小值此时s=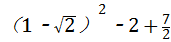 =
= .
.故当
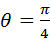 ,最小值为
,最小值为 ;(6分)
;(6分)(II)∵
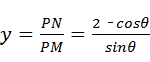
∴
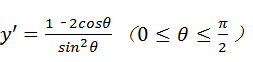 ,令1﹣2cosθ=0⇒
,令1﹣2cosθ=0⇒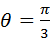 .
.| θ | 0 | 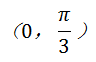 | 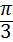 | 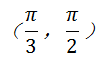 |  |
 | | ﹣ ↘ | 0 极小 | + ↗ | |
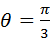 时,
时,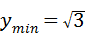 (12分)
(12分)略

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
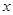 轴上的双曲线的渐近线方程是
轴上的双曲线的渐近线方程是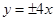 ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )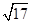
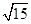
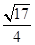
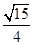
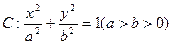 的离心率为
的离心率为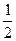 ,且经过点
,且经过点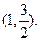
 过右焦点F与椭圆C交于M,N两点,若AM、AN的斜率
过右焦点F与椭圆C交于M,N两点,若AM、AN的斜率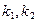 满足
满足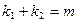 (定值
(定值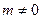 ),求直线
),求直线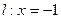 相切。
相切。 的直线与曲线M相交于A,B两点,A,B在直线
的直线与曲线M相交于A,B两点,A,B在直线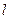 上的射影是
上的射影是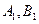 。求梯形
。求梯形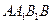 的面积;
的面积;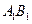 上的动点,当△ABC为直角三角形时,求点C的坐标。
上的动点,当△ABC为直角三角形时,求点C的坐标。 是椭圆
是椭圆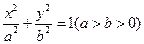 的左、右焦点,过点
的左、右焦点,过点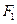 作
作 的直线
的直线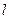 交椭圆于
交椭圆于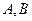 两点,
两点,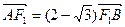 .
.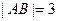 ,求椭圆的标准方程.
,求椭圆的标准方程.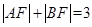 ,则线
,则线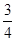
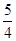
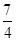
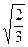 ,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段
,过点C(-1,0)的直线l与椭圆E相交于A、B两点,且C分有向线段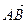 的比为2.
的比为2.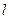 与抛物线
与抛物线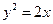 交于点
交于点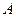 、
、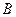 ,以线段
,以线段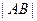 为直径的圆
为直径的圆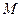 恰与抛物线
恰与抛物线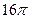 ,则直线
,则直线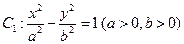 的左、右焦点分别为
的左、右焦点分别为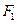 、
、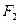 ,抛物线
,抛物线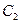 的顶点在原点,它的准线与双曲线
的顶点在原点,它的准线与双曲线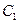 的左准线重合,若双曲线
的左准线重合,若双曲线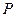 满足
满足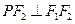 ,则双曲线
,则双曲线