题目内容
(本小题满分14分)已知椭圆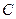 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在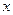 轴上,长轴长为
轴上,长轴长为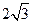 ,离心率为
,离心率为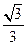 ,经过其左焦点
,经过其左焦点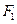 的直线
的直线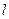 交椭圆
交椭圆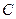 于
于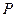 、
、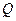 两点(I)求椭圆
两点(I)求椭圆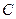 的方程;
的方程;
(II)在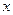 轴上是否存在一点
轴上是否存在一点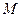 ,使得
,使得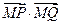 恒为常数?若存在,求出
恒为常数?若存在,求出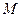 点的坐标和这个常数;若不存在,说明理由.
点的坐标和这个常数;若不存在,说明理由.
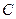 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在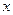 轴上,长轴长为
轴上,长轴长为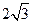 ,离心率为
,离心率为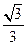 ,经过其左焦点
,经过其左焦点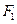 的直线
的直线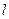 交椭圆
交椭圆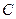 于
于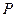 、
、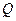 两点(I)求椭圆
两点(I)求椭圆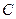 的方程;
的方程;(II)在
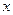 轴上是否存在一点
轴上是否存在一点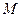 ,使得
,使得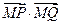 恒为常数?若存在,求出
恒为常数?若存在,求出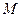 点的坐标和这个常数;若不存在,说明理由.
点的坐标和这个常数;若不存在,说明理由.解:(I)设椭圆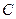 的方程为
的方程为 .
.
由题意,得 ,解得
,解得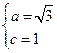 ,所以
,所以 . …………………2分
. …………………2分
所求的椭圆方程为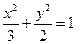 . …………………………………………………4分
. …………………………………………………4分
(II)由(I)知 . 假设在
. 假设在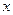 轴上存在一点
轴上存在一点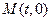 ,使得
,使得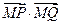 恒为常数
恒为常数
①当直线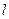 与
与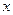 轴不垂直时,设其方程为
轴不垂直时,设其方程为 ,
, 、
、 .
.
由 得
得 . ……………………………5分
. ……………………………5分
所以 ,
, . ……………
. …………… …………………………6分
…………………………6分
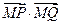


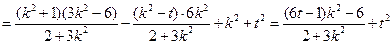
 .
.
因为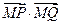 是与
是与 无关的常数,从而有
无关的常数,从而有 ,即
,即 . ……………9分
. ……………9分
此时 . …………………………………………………11分
. …………………………………………………11分
②当直线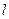 与
与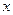 轴垂直时,此时点
轴垂直时,此时点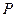 、
、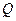 的坐标分别为
的坐标分别为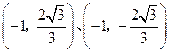 ,
,
当 时,亦有
时,亦有 . ……
. …… ………………………13分
………………………13分
综上,在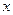 轴上存在定点
轴上存在定点 ,使得
,使得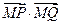 恒为常数,且这个常数为
恒为常数,且这个常数为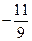 .
.
……………………………14分
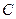 的方程为
的方程为 .
. 由题意,得
 ,解得
,解得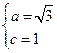 ,所以
,所以 . …………………2分
. …………………2分所求的椭圆方程为
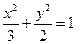 . …………………………………………………4分
. …………………………………………………4分(II)由(I)知
 . 假设在
. 假设在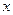 轴上存在一点
轴上存在一点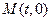 ,使得
,使得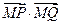 恒为常数
恒为常数①当直线
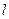 与
与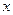 轴不垂直时,设其方程为
轴不垂直时,设其方程为 ,
, 、
、 .
.由
 得
得 . ……………………………5分
. ……………………………5分所以
 ,
, . ……………
. …………… …………………………6分
…………………………6分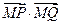


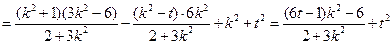
 .
.因为
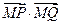 是与
是与 无关的常数,从而有
无关的常数,从而有 ,即
,即 . ……………9分
. ……………9分此时
 . …………………………………………………11分
. …………………………………………………11分②当直线
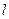 与
与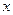 轴垂直时,此时点
轴垂直时,此时点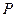 、
、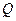 的坐标分别为
的坐标分别为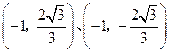 ,
,当
 时,亦有
时,亦有 . ……
. …… ………………………13分
………………………13分综上,在
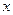 轴上存在定点
轴上存在定点 ,使得
,使得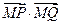 恒为常数,且这个常数为
恒为常数,且这个常数为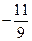 .
.……………………………14分
略

练习册系列答案
相关题目
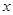 轴上的双曲线的渐近线方程是
轴上的双曲线的渐近线方程是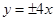 ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )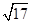
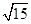
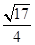
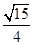
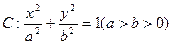 的离心率为
的离心率为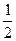 ,且经过点
,且经过点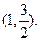
 过右焦点F与椭圆C交于M,N两点,若AM、AN的斜率
过右焦点F与椭圆C交于M,N两点,若AM、AN的斜率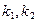 满足
满足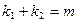 (定值
(定值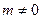 ),求直线
),求直线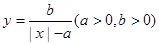 与
与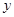 轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为 .
轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当a=1,b=1时,所有的“望圆”中,面积最小的“望圆”的面积为 .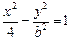
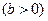 的渐近线方程式为
的渐近线方程式为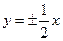 ,则
,则 等于
等于 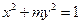 的焦点在
的焦点在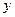 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则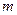 的值为________
的值为________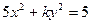 的一个焦点是
的一个焦点是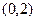 ,那么
,那么