题目内容
已知数列 满足
满足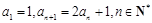 .
.
(1)证明数列 为等比数列,并求出数列
为等比数列,并求出数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 .证明:数列
.证明:数列 是等差数列.
是等差数列.
(3)证明: .
.
 满足
满足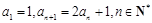 .
.(1)证明数列
 为等比数列,并求出数列
为等比数列,并求出数列 的通项公式;
的通项公式;(2)若数列
 满足
满足 .证明:数列
.证明:数列 是等差数列.
是等差数列.(3)证明:
 .
.(1)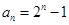 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
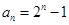 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.试题分析:(1)证明数列
 为等比数列,就是证明
为等比数列,就是证明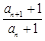 为一个常数. 因为
为一个常数. 因为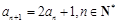 ,所以
,所以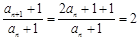 ,所以,
,所以,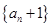 是以2为首项,2为公比的等比数列. 则
是以2为首项,2为公比的等比数列. 则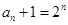 ,即
,即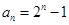 ,
,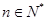 ;(2)证明数列
;(2)证明数列 是等差数列,就是要证明
是等差数列,就是要证明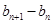 为一个常数.首先化简等式
为一个常数.首先化简等式 ,即
,即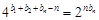 ,所以
,所以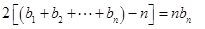 ,这实质是
,这实质是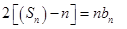 ,因此作差消去
,因此作差消去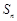 得:
得: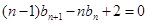 ,再作差消去常数得:
,再作差消去常数得: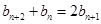 ,
,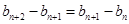 ,即
,即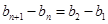 ;(3)证明数列不等式,一般有两个思路,一是求和,二是放缩.本题由于通项
;(3)证明数列不等式,一般有两个思路,一是求和,二是放缩.本题由于通项 不适宜求和,所以尝试放缩,即利用变量分离进行放缩,由
不适宜求和,所以尝试放缩,即利用变量分离进行放缩,由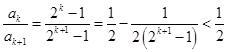 ,得
,得 .
.试题解析:(1)因为
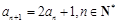 ,所以
,所以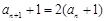 ,且
,且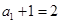 ,
,所以,
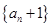 是以2为首项,2为公比的等比数列. 2分
是以2为首项,2为公比的等比数列. 2分则
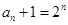 ,即
,即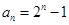 ,
,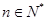 . 3分
. 3分(2)因为
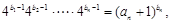 所以.
所以.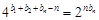 4分
4分所以
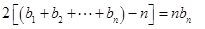 ①
①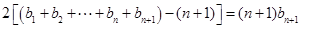 ② 6分
② 6分②-①,得
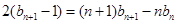
即
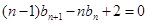 ③
③ 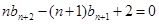 ④ 8分
④ 8分④-③,得
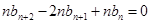 ,
,即
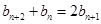
得
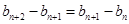 ,
,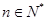 10分
10分所以数列
 为等差数列.
为等差数列.(3)因为
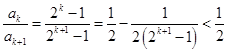 ,
,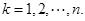 11分
11分所以
 . 12分
. 12分
练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
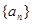 的前n项和为Sn,且满足
的前n项和为Sn,且满足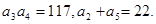
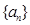 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列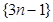 的一个是等比数列的子列;
的一个是等比数列的子列;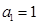 ,公比
,公比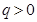 且
且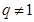 ,则数列
,则数列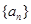 为等差数列,
为等差数列,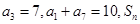 为其前n项和,则使得
为其前n项和,则使得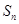 达到最大值的n等于 .
达到最大值的n等于 . 间的整数
间的整数 为分子,以
为分子,以 为分母组成分数集合
为分母组成分数集合 ,其所有元素和为
,其所有元素和为 ;以
;以 间的整数
间的整数 为分母组成不属于集合
为分母组成不属于集合 ,其所有元素和为
,其所有元素和为 ;……,依次类推以
;……,依次类推以 间的整数
间的整数 为分母组成不属于
为分母组成不属于 的分数集合
的分数集合 ,其所有元素和为
,其所有元素和为 ;则
;则 =________.
=________.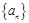 的前
的前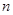 项和为
项和为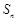 ,首项
,首项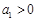 ,
,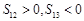 .则以下关于数列
.则以下关于数列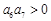 ;②
;②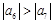 ;③
;③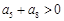 ;④前
;④前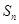 中最大的项为第六项
中最大的项为第六项 满足:
满足: ,则其前10项的和
,则其前10项的和 ( )
( )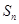 是等差数列
是等差数列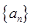 的前
的前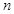 项和,公差
项和,公差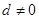 ,若
,若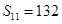 ,若
,若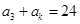 ,则正整数
,则正整数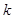 的值为( )
的值为( )



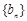 为等差数列,
为等差数列,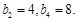 数列
数列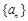 满足
满足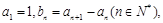 则
则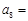 ( )
( )