题目内容

8．一条直线与两条相交直线成等角，那么这条直线与这两条相交直线的位置关系是相交或异面．

分析 以正方体为载体，能判断出这条直线与这两条相交直线的位置关系．

解答 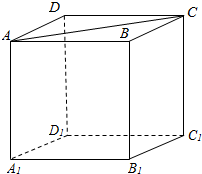解：正方体ABCD-A1B1C1D1中，AD∩AB=A，
AC与AD和AB所成角相等，AC与AD和AB相交；
A1C1与AD和AB所成角相等，A1C1与AD和AB异面．
∴一条直线与两条相交直线成等角，
那么这条直线与这两条相交直线的位置关系是相交或异面．
故答案为：相交或异面．

点评 本题考查直线与两条相交直线的位置关系的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
18．若a=log${\;}_{\frac{1}{3}}$2，b=log${\;}_{\frac{1}{2}}$$\frac{1}{3}$，c=（$\frac{1}{2}$）0.3，则，a，b，c的大小关系为a＜c＜b．
19．对于函数f（x），若存在x0∈R，使得f（x0）=x0成立，则称x0为f（x）的“滞点”．己知函数f（x）=$\frac{2{x}^{2}-a}{x-2a}$，若f（x）在x∈[-1，1]内存在“滞点”，求a的取值范围．
16．证明：sin（π+α）sin（π-α）+cos（3π+α）cos（4π-α）=-1．
3．（2x+5）2＜36的解集是{x|$-\frac{11}{2}＜x＜\frac{1}{2}$}．
13．已知f（x）=$\frac{{e}^{x}+lo{g}_{a}x}{cosx}$（a＞0，a≠1），f′（π）=-eπ-$\frac{1}{π}$，则a=e．
20．若xlog34=1，则$\frac{{2}^{2x}-{2}^{-2x}}{{2}^{x}+{2}^{-x}}$=$\frac{2}{3}$$\sqrt{3}$．
17．已知函数y=f（x）是奇函数，且f（1）=2，则函数y=f（x）图象必过点（　　）
A．（-1，2）B．（2，1）C．（-1，-2）D．（-2，-1）
18．若函数f（x）=x2014，则f′（（$\frac{1}{2014}$）${\;}^{\frac{1}{2013}}$）=（　　）
A．0B．1C．2014D．2013

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网