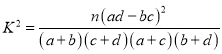题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() ,曲线
,曲线![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 的极坐标方程为
的极坐标方程为![]() ,若
,若![]() 分别与
分别与![]() 交于异于极点的
交于异于极点的![]() 两点,求
两点,求![]() 的最大值.
的最大值.
【答案】(1)![]() 的极坐标方程是
的极坐标方程是![]() ,
,![]() 的极坐标方程是
的极坐标方程是![]() . (2)
. (2)![]()
【解析】
(1)利用![]() 将
将![]() 的直角坐标方程化为极坐标方程;先把
的直角坐标方程化为极坐标方程;先把![]() 的参数方程化为普通方程,再化为极坐标方程;
的参数方程化为普通方程,再化为极坐标方程;
(2)分别联立曲线![]() 与
与![]() 的极坐标方程与
的极坐标方程与![]() ,即可求得
,即可求得![]() ,
,![]() ,再利用二次函数的性质求得
,再利用二次函数的性质求得![]() 的最大值,进而求解.
的最大值,进而求解.
解:(1)因为![]() ,
,
所以![]() 可化为
可化为![]() ,
,
整理得![]() ,
,
![]() (
(![]() 为参数),则
为参数),则![]() (
(![]() 为参数),化为普通方程为
为参数),化为普通方程为![]() ,则极坐标方程为
,则极坐标方程为![]() ,即
,即![]() .
.
所以![]() 的极坐标方程是
的极坐标方程是![]() ,
,![]() 的极坐标方程是
的极坐标方程是![]() .
.
(2)由(1)知,
联立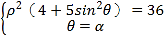 可得
可得![]() ,
,
联立![]() 可得
可得![]() ,
,
所以![]()
![]() ,
,
当![]() 时,
时,![]() 最大值为
最大值为![]() ,所以
,所以![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某科研团队对![]() 例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中
例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中![]() 名吸烟患者中,重症人数为
名吸烟患者中,重症人数为![]() 人,重症比例约为
人,重症比例约为![]() ;
;![]() 名非吸烟患者中,重症人数为
名非吸烟患者中,重症人数为![]() 人,重症比例为
人,重症比例为![]() .根据以上数据绘制
.根据以上数据绘制![]() 列联表,如下:
列联表,如下:
吸烟人数 | 非吸烟人数 | 总计 | |
重症人数 | 30 | 120 | 150 |
轻症人数 | 100 | 800 | 900 |
总计 | 130 | 920 | 1050 |
(1)根据列联表数据,能否在犯错误的概率不超过![]() 的前提下认为新冠肺炎重症和吸烟有关?
的前提下认为新冠肺炎重症和吸烟有关?
(2)已知每例重症患者平均治疗费用约为![]() 万元,每例轻症患者平均治疗费用约为
万元,每例轻症患者平均治疗费用约为![]() 万元.现有吸烟确诊患者20人,记这
万元.现有吸烟确诊患者20人,记这![]() 名患者的治疗费用总和为
名患者的治疗费用总和为![]() ,求
,求![]() .
.
附:
|
|
|
|
|
|
|
|